Καθετότητα ευθειών

#1

Σε ένα οξυγώνιο τρίγωνο $\triangle ABC$ , AB>AC

, και

,

είναι το περίκεντρο και το ορθόκεντρο, αντίστοιχα. Έστω

το μέσο της πλευράς

, έστω

το σημείο τομής της επέκτασης της

με τον περιγεγραμμένο κύκλο του BHC

, και έστω

το σημείο τομής της

και της

. Να δειχθεί ότι αν $B\widehat{A}M=C\widehat{A}N$ , τότε $AN\perp OH$ .

ΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ · #2

achilleas έγραψε: ↑
Σάβ Απρ 08, 2023 10:11 am
Σε ένα οξυγώνιο τρίγωνο $\triangle ABC$ , , και , είναι το περίκεντρο και το ορθόκεντρο, αντίστοιχα. Έστω το μέσο της πλευράς , έστω το σημείο τομής της επέκτασης της με τον περιγεγραμμένο κύκλο του , και έστω το σημείο τομής της και της . Να δειχθεί ότι αν $B\widehat{A}M=C\widehat{A}N$ , τότε $AN\perp OH$ .

Ως γνωστών η τομή του $\odot(HBC)$ με την

είναι το

point και $HT\perp AM$ .

Άρα το κέντρο O_1

του $\odot(HBC)$ είναι πάνω στην

και είναι το συμμετρικό του

ως προς

.
Έτσι αν

το ίχνος του ύψους από το

τότε αφού

μέσο

και $HD\parallel OO_1$ έχω H(O,M,O_1,D)=-1

άρα

όπου

η τομή

με

.
Τώρα

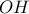, θεωρώ "συμμετρία" ως προς τη διχοτόμο της

(διατηρεί διπλό λόγο), οπότε N,M

αλλάζουν μεταξύ τους θέσεις και

πάει

αλλά

μέσον

αφού $HO_1\parallel AO$ έτσι η συμμετρική της

προς τη διχοτόμο της

είναι η παράλληλη προς τη

, αλλά αυτό γίνεται όταν η

είναι η εφαπόμενη στον περίκυκλο στο

και τώρα το ζητούμενο είναι άμεσο μιας και η

από την υπόθεση είναι συμμετροδιάμεσος και είναι και η πολική του

προς τον περίκυκλο οπότε θα πρέπει $OU\perp AN$ .

Ορέστης Λιγνός · #3

Η λύση του Πρόδρομου είναι πολύ συνθετική για τα γούστα μου, οπότε γράφω μία με bash

Αρχικά, είναι

$\angle BKC=180^\circ-\angle BHC=\angle BAC,$

και αφού $K \in AM$ , το σημείο

είναι το συμμετρικό του

ως προς το

.

Τώρα, αφού $\angle BAM=\angle CAN,$ η

είναι η συμμετροδιάμεσος. Από το Ratio Lemma και τις ιδιότητες τις συμμετροδιάμεσου έχουμε ότι

$\dfrac{c^2}{b^2}=\dfrac{BN}{NC}=\dfrac{BH}{HC} \cdot \dfrac{\sin \angle BHN}{\sin \angle NHC}=\dfrac{\cos \angle B}{\cos \angle C} \cdot \dfrac{BK}{KC}=\dfrac{(a^2+c^2-b^2)b}{(a^2+b^2-c^2)c} \cdot \dfrac{b}{c},$

και άρα (a^2+c^2-b^2)b^4=(a^2+b^2-c^2)c^4,

συνεπώς

και αφού

προκύπτει ότι a^2(b^2+c^2)=b^4+c^4

.

Έστω τώρα ότι η εφαπτομένη του κύκλου (ABC)

στο σημείο

τέμνει την

στο σημείο

.

Ισχυρισμός: Τα τρίγωνα AHO

και

είναι όμοια.
Απόδειξη: Είναι,

$\angle OAH=\angle BAH-\angle BAO=(90^\circ-\angle B)-(90^\circ-\angle C)=\angle C-\angle B,$

και

$\angle AQM=\angle C-\angle CAQ=\angle C-\angle B,$

οπότε $\angle OAH=\angle AQM$ . Για να δείξουμε λοιπόν ότι τα δύο τρίγωνα είναι όμοια, αρκεί να δείξουμε ότι

$\dfrac{AH}{AO}=\dfrac{QA}{QM}$ .

Είναι,

$\dfrac{AH}{AO}=\dfrac{2OM}{BO}=2\cos \angle A=\dfrac{b^2+c^2-a^2}{bc}.$

Επιπλέον, τα τρίγωνα QAC

και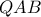

είναι όμοια, συνεπώς $\dfrac{QA}{QB}=\dfrac{QC}{QA}=\dfrac{b}{c},$ οπότε εύκολα προκύπτει ότι $\dfrac{QB}{QC}=\dfrac{b^2}{c^2},$ που δίνει πως

$QB=\dfrac{ac^2}{b^2-c^2}, QC=\dfrac{ab^2}{b^2-c^2}$ και $QA=\dfrac{abc}{b^2-c^2}$ .

Έτσι,

$\dfrac{QA}{QM}=\dfrac{QA}{QC+\dfrac{a}{2}}=\ldots=\dfrac{2bc}{b^2+c^2}.$

Συνεπώς, αρκεί να αποδείξουμε ότι $\dfrac{b^2+c^2-a^2}{bc}=\dfrac{2bc}{b^2+c^2},$ η ισοδύναμα ότι a^2(b^2+c^2)=b^4+c^4,

που έχουμε αποδείξει ότι ισχύει $\blacksquare$

Στο πρόβλημα από το αποτέλεσμα του Ισχυρισμού είναι

$\angle MAQ=\angle OHA,$ συνεπώς

$\angle OHA+\angle NAH=\angle OHA+\angle NAC-\angle HAC=\angle MAQ+\angle NAC-\angle OAB=$

$=90^\circ-\angle MAO+\angle NAC-\angle OAB=90^\circ-\angle MAB+\angle NAC=90^\circ,$

και άρα $\angle OHA+\angle NAH=90^\circ,$ που δίνει ότι οι

και

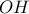είναι κάθετες, όπως δηλαδή θέλαμε.

#4

Επιπλέον πληροφορίες για την άσκηση:

$\displaystyle \bullet$ Με το συνήθη συμβολισμό των πλευρών τριγώνου είναι AN=b

και $\displaystyle a = b\sqrt 2 = c\sqrt {2(\sqrt 2 - 1)}$

$\displaystyle \bullet$ Για τις ίσες γωνίες $B\widehat AM=C\widehat AN=\theta,$ είναι $\displaystyle \cos \theta = \sqrt 2 - \frac{1}{2}$

Τέλος η άσκηση λύνεται και με τη συνθήκη καθετότητας $\displaystyle O{A^2} - O{N^2} = BN \cdot NC = H{A^2} - H{N^2}$ αφού

πρώτα αποδειχθεί ότι η

εφάπτεται στον περίκυκλο του τριγώνου ANK,...

κλπ. (έχει όμως πολύ γράψιμο).

#5

achilleas έγραψε: ↑
Σάβ Απρ 08, 2023 10:11 am
Σε ένα οξυγώνιο τρίγωνο $\triangle ABC$ , , και , είναι το περίκεντρο και το ορθόκεντρο, αντίστοιχα. Έστω το μέσο της πλευράς , έστω το σημείο τομής της επέκτασης της με τον περιγεγραμμένο κύκλο του , και έστω το σημείο τομής της και της . Να δειχθεί ότι αν $B\widehat{A}M=C\widehat{A}N$ , τότε $AN\perp OH$ .

Ας δούμε και μια διαφορετική με στοιχειώδη μέσα προσέγγιση της πολύ όμορφης πρότασης του Αχιλλέα

$\bullet$ Με $\angle BHC={{180}^{0}}-\angle BAC$ (από το ορθόκεντρο

του $\vartriangle ABC$ ) προκύπτει ότι οι περίκυκλοι $\left( O \right),\left( {{O}'} \right)$ των τριγώνων $\vartriangle ABC,\vartriangle HBC$ είναι ίσοι (τα σημεία τους A,H

«βλέπουν» την κοινή τους χορδή υπό παραπληρωματικές γωνίες) , συμμετρικοί ως προς την

με κέντρο συμμετρίας το μέσο

της εν λόγω χορδής και συνεπως $MA=MK:\left( 1 \right)$

$\bullet$ Από το θεώρημα του Μενελάου στο τρίγωνο $\vartriangle AMD$ (με $D\equiv AH\cap BC$ ) με διατέμνουσα την KNH

προκύπτει ότι $\dfrac{KM}{KA}\cdot \dfrac{HA}{HD}\cdot \dfrac{ND}{NM}=1:\left( 2 \right)$ και από την $\left( 1 \right)\Rightarrow KA=2KM$ και με HA=2OM

(γνωστή πρόταση) η σχέση $\left( 2 \right)$ γίνεται $\dfrac{KM}{2KM}\cdot \dfrac{2OM}{HD}\cdot \dfrac{ND}{NM}=1\Rightarrow \ldots \dfrac{OM}{HD}=\dfrac{NM}{ND}:\left( 3 \right)$

Από την $\left( 3 \right)$ προκύπτει ότι τα ορθογώνια τρίγωνα $\vartriangle OMN,\vartriangle HDN$ είναι όμοια (κάθετες πλευρές ανάλογες) και συνεπώς $\angle ONM=\angle HND:\left( 4 \right)$

: Κάθετες ευθείες.png (40.79 KiB) Προβλήθηκε 923 φορές

$\bullet$ Αν $F\equiv AH\cap \left( O \right),F\ne A$ είναι γνωστό ότι

το συμμετρικό του

ως προς την

και συνεπώς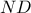

μεσοκάθετη της $HF\Rightarrow \angle FND=\angle HND\overset{\left( 4 \right)}{\mathop{=}}\,\angle ONM\overset{M,N,D\,\,\sigma \upsilon \nu \varepsilon \upsilon \theta \varepsilon \iota \alpha \kappa \alpha }{\mathop{\Rightarrow }}\,O,N,F$ συνευθειακά και συνεπώς $\angle OAF\overset{OA=OF={{R}_{O}}}{\mathop{=}}\,\angle AFO\equiv \angle HFN\overset{NF=NH}{\mathop{=}}\,\angle NHF\Rightarrow HN\parallel OA$ και με $HA\parallel OM$ (κάθετες στην

) προκύπτει ότι $\angle AHN=\angle AOM:\left( 5 \right)$ και εφόσον οι AO,AH

είναι ισογώνιες (γνωστή πρόταση) ως προς τις πλευρές της γωνίας $\angle BAC$ και $\angle NAC=\angle MAB$ θα είναι και $\angle NAH=\angle MAO:\left( 6 \right)$ (διαφορά ίσων γωνιών)

$\bullet$ Από $\left( 5 \right),\left( 6 \right)\Rightarrow \vartriangle AHN\sim \vartriangle AOM\Rightarrow \dfrac{AH}{AO}=\dfrac{AN}{AM}:\left( 7 \right)$
Αν

είναι η ορθή προβολή του

στην ευθεία

για τα ορθογώνια τρίγωνα $\vartriangle NEA,\vartriangle MDA$ στα H,D

αντίστοιχα, είναι και $\angle EAN=\angle EAM+\angle MAN=\angle NAD+\angle MAN=\angle DAM$ οπότε είναι όμοια και συνεπώς $\dfrac{AE}{AD}=\dfrac{AN}{AM}\overset{\left( 7 \right)}{\mathop{\Rightarrow }}\,\dfrac{AE}{AD}=\dfrac{AH}{AO}:\left( 8 \right)$

$\bullet$ Από την $\left( 8 \right)$ σύμφωνα με το Stathis Koutras Theorem προκύπτει ότι $AN\bot OH$ και το ζητούμενο έχει αποδειχθεί .

Henri van Aubel · #6

achilleas έγραψε: ↑
Σάβ Απρ 08, 2023 10:11 am
Σε ένα οξυγώνιο τρίγωνο $\triangle ABC$ , , και , είναι το περίκεντρο και το ορθόκεντρο, αντίστοιχα. Έστω το μέσο της πλευράς , έστω το σημείο τομής της επέκτασης της με τον περιγεγραμμένο κύκλο του , και έστω το σημείο τομής της και της . Να δειχθεί ότι αν $B\widehat{A}M=C\widehat{A}N$ , τότε $AN\perp OH$ .

Γειά χαρά Αχιλλέα!

Βάζω μία λύση χωρίς καθόλου πείραγμα του σχήματος. Πάμε μία στα γρήγορα.

Έχουμε $\displaystyle ON^{2}=\left ( \frac{ac^{2}}{b^{2}+c^{2}} \right )^{2}+AO^{2}-\frac{a^{2}c^{2}}{b^{2}+c^{2}}=AO^{2}-\frac{a^{2}b^{2}c^{2}}{\left ( b^{2}+c^{2} \right )^{2}}\left ( 1 \right ).$

Εξάλλου, $\displaystyle HN^{2}=HC^{2}+\left ( \frac{ab^{2}}{b^{2}+c^{2}} \right )^{2}-\frac{a^{2}+b^{2}-c^{2}}{a}\cdot \frac{ab^{2}}{b^{2}+c^{2}}=HC^{2}-\frac{b^{2}\left ( a^{2}c^{2}+b^{4}-c^{4} \right )}{\left ( b^{2}+c^{2} \right )^{2}}\left ( 2 \right ).$

Από τις $\left ( 1 \right ),\left ( 2 \right )$ θα είναι $\displaystyle ON^{2}-HN^{2}=AO^{2}-HC^{2}+\frac{b^{2}\left ( b^{2}-c^{2} \right )}{b^{2}+c^{2}}\left ( 3 \right ).$

Όμως θέλουμε για να είναι $AN\perp OH$ να είναι και $ON^{2}-HN^{2}=AO^{2}-AH^{2}.$

Συνεπώς, αρκεί $\displaystyle AO^{2}-HC^{2}+\frac{b^{2}\left ( b^{2} -c^{2}\right )}{b^{2}+c^{2}}=AO^{2}-AH^{2}\Leftrightarrow AH^{2}-HC^{2}=\frac{b^{2}\left ( c^{2}-b^{2} \right )}{b^{2}+c^{2}}.$

Επειδή $BH\perp AC\Longrightarrow AH^{2}-HC^{2}=AB^{2}-BC^{2}=c^{2}-a^{2}$ , έπεται πως αρκεί $\displaystyle c^{2}-a^{2}=\frac{b^{2}\left ( c^{2} -b^{2}\right )}{b^{2}+c^{2}}\left ( I \right ).$

Όμως, είναι $\displaystyle \frac{BN}{NC}=\frac{BH}{HC}\cdot \frac{\sin \angle BHK}{\sin \angle CHK}\Leftrightarrow \frac{c^{2}}{b^{2}}=\frac{\cos B}{\cos C}\cdot \frac{b}{c}=\frac{a^{2}+c^{2}-b^{2}}{a^{2}+b^{2}-c^{2}}\cdot \frac {b^{2}}{c^{2}}\left ( II \right ).$

Σουλουπώνοντας λίγο την $\left ( II \right )$ θα έχουμε $\displaystyle b^{4}\left ( a^{2} +c^{2}-b^{2}\right )=c^{4}\left ( a^{2}+b^{2}-c^{2} \right )\Leftrightarrow c^{2}-a^{2}=\frac{b^{2}\left ( c^{2}-b^{2} \right )}{b^{2}+c^{2}}\left ( II \right ).$

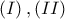Οπότε από τις $\left ( I \right ),\left ( II \right )$ δείξαμε ότι $ON^{2}-HN^{2}=AO^{2}-AH^{2}\Longrightarrow AN\perp OH.$

Καθετότητα ευθειών

Καθετότητα ευθειών

Re: Καθετότητα ευθειών

Re: Καθετότητα ευθειών

Re: Καθετότητα ευθειών

Re: Καθετότητα ευθειών

Re: Καθετότητα ευθειών

Μέλη σε σύνδεση