Έστω

τα πρίσματα, όχι απαραίτητα ορθά, που κατασκεάσαμε στις έδρες

αντίστοιχα και

το σημείο τομής των επιπέδων, που ορίζουν οι έδρες

.
Έστω επίση

το πρίσμα με ακμές παράλληλες και ίσες με το τμήμα

και βάση την έδρα

.
Επειδή

το τετράπλευρο

είναι παραλληλόγραμμο και θα ισχύει

. Ομοίως βρίσκουμε, ότι

και

.
Το επίπεδο

είναι παράλληλο στο επίπεδο
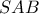
και το επίπεδο

είναι παράλληλο στο επίπεδο

. Άρα η τομή των επιπέδων

και

, που είναι ευθεία, έστω η

, θα είναι παράλληλη στην τομή των επιπέδων
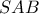
και

.
Η ευθεία

είναι παράλληλη προς την

και διέρχεται από το

. Όμως και η

είναι παράλληλη προς την

και διέρχεται από το σημείο

. Άρα το σημείο

βρίσκεται στην ευθεία

.
Ομοίως βρίσκουμε ότι το σημείο

βρίσκεται στην ευθεία

, που είναι η τομή των επιπέδων

και

. Το σημείο

βρίσκεται στην αντίστοιχη ευθεία

, τομή των επιπέδων

και

.
Επομένως τα
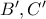
βρίσκονται στο ίδιο επίπεδο με την έδρα

. Άρα το πρίσμα

είναι ισοδύναμο με το πρίσμα

.
Ομοίως βρίσκουμε, ότι τo πρίσμα

είναι ισοδύναμο με το πρίσμα

και το πρίσμα

ισοδύναμο με το

.
Από τις παραλληλίες και ισότητες παραπάνω συμπεραίνουμε ότι τα τετράεδρα

και

είναι ίσα, ως παράλληλη μεταφορά του ενός στο άλλο.
Οπότε ο συνολικός όγκος των αρχικών πρισμάτων που κατασκευάσαμε ισούται με τον όγκο του στερεού που περικλείεται από τις τρίεδρες γωνίες

και

και παράπλευρες έδρες, που ορίζονται από τα τμήματα

.
Άρα, εν τέλη, ο όγκος του παραπάνω στερεού ισούται με τον όγκο του πρίσματος

, που είναι το ζητούμενο.

- isodunamia_r3.png (180.17 KiB) Προβλήθηκε 390 φορές
 και επί των εδρών του
και επί των εδρών του  και προς τα έξω κατασκευάζουμε τρία πρίσματα. Αν
και προς τα έξω κατασκευάζουμε τρία πρίσματα. Αν  είναι η τομή των πάνω βάσεων των πρισμάτων αυτών, κατασκευάζουμε επί της τέταρτης έδρας
είναι η τομή των πάνω βάσεων των πρισμάτων αυτών, κατασκευάζουμε επί της τέταρτης έδρας  πρίσμα που η παράπλευρη ακμή του είναι ίση και παράλληλη προς την
πρίσμα που η παράπλευρη ακμή του είναι ίση και παράλληλη προς την  Να αποδείξετε ότι το πρίσμα αυτό είναι ισοδύναμο με το άθροισμα των τριών άλλων πρισμάτων.
Να αποδείξετε ότι το πρίσμα αυτό είναι ισοδύναμο με το άθροισμα των τριών άλλων πρισμάτων. 
 του τετραέδρου
του τετραέδρου  και είναι ορθά με αντίστοιχα ύψη
και είναι ορθά με αντίστοιχα ύψη  .
.  του δοθέντος τετραέδρου
του δοθέντος τετραέδρου  , όπου
, όπου  είναι η τομή των τριών επιπέδων των επάνω βάσεων των
είναι η τομή των τριών επιπέδων των επάνω βάσεων των  και ύψος
και ύψος 

 όπου
όπου  είναι η τομή της
είναι η τομή της  με
με  .
.  παράλληλα προς την απέναντι έδρα και προκύπτει
παράλληλα προς την απέναντι έδρα και προκύπτει  και ύψος το
και ύψος το  καθόσον εύκολα φαίνεται ότι
καθόσον εύκολα φαίνεται ότι  είναι ίσα.
είναι ίσα. τα πρίσματα, όχι απαραίτητα ορθά, που κατασκεάσαμε στις έδρες
τα πρίσματα, όχι απαραίτητα ορθά, που κατασκεάσαμε στις έδρες  .
. το πρίσμα με ακμές παράλληλες και ίσες με το τμήμα
το πρίσμα με ακμές παράλληλες και ίσες με το τμήμα  και βάση την έδρα
και βάση την έδρα  το τετράπλευρο
το τετράπλευρο  είναι παραλληλόγραμμο και θα ισχύει
είναι παραλληλόγραμμο και θα ισχύει  . Ομοίως βρίσκουμε, ότι
. Ομοίως βρίσκουμε, ότι  και
και  .
. είναι παράλληλο στο επίπεδο
είναι παράλληλο στο επίπεδο 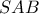 και το επίπεδο
και το επίπεδο  είναι παράλληλο στο επίπεδο
είναι παράλληλο στο επίπεδο  . Άρα η τομή των επιπέδων
. Άρα η τομή των επιπέδων  , θα είναι παράλληλη στην τομή των επιπέδων
, θα είναι παράλληλη στην τομή των επιπέδων  και διέρχεται από το
και διέρχεται από το  είναι παράλληλη προς την
είναι παράλληλη προς την  βρίσκεται στην ευθεία
βρίσκεται στην ευθεία  βρίσκεται στην ευθεία
βρίσκεται στην ευθεία  , που είναι η τομή των επιπέδων
, που είναι η τομή των επιπέδων  . Το σημείο
. Το σημείο  βρίσκεται στην αντίστοιχη ευθεία
βρίσκεται στην αντίστοιχη ευθεία  , τομή των επιπέδων
, τομή των επιπέδων 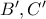 βρίσκονται στο ίδιο επίπεδο με την έδρα
βρίσκονται στο ίδιο επίπεδο με την έδρα  είναι ισοδύναμο με το πρίσμα
είναι ισοδύναμο με το πρίσμα  .
. είναι ισοδύναμο με το πρίσμα
είναι ισοδύναμο με το πρίσμα  και το πρίσμα
και το πρίσμα  ισοδύναμο με το
ισοδύναμο με το  .
. είναι ίσα, ως παράλληλη μεταφορά του ενός στο άλλο.
είναι ίσα, ως παράλληλη μεταφορά του ενός στο άλλο.  .
.