Όσο πιο κοντά στην αρχή

KARKAR · #1

: Όσο πιο κοντά στην αρχή.png (8.28 KiB) Προβλήθηκε 312 φορές

Στο ορθογώνιο τρίγωνο ABC

, με :

, το

είναι το ύψος προς την υποτείνουσα

.

Σημείο

κινείται στο εσωτερικό του τμήματος

. Η κάθετη προς το τμήμα

στο

, τέμνει την

,

στο σημείο

. Βρείτε το ελάχιστο μήκος του τμήματος

. Γενίκευση για : AC=b , AB=c , b<c

.

Pi3.1415 · #2

Α) Φέρνω τον περιεγγεγραμμένο κύκλο του τριγώνου AST. Αφού $\angle AST=90^{\circ}$ , η ΑΤ είναι διάμετρος και αρκεί να βρούμε το σημείο S όπου ο περιεγγεγραμμένος κύκλος είναι ο ελάχιστος. Με ΠΘ στο ACD και στο ADB βρίσκω $AD=\frac{60}{13}$ , $CD=\frac{50}{26}$ . Θέτω DS=x

. Έτσι από ΠΘ στο ADS έχω $AS=\sqrt{x^2+\frac{3600}{169}}$ . Από γνωστό θεώρημα ξέρουμε πως $\angle ACD=\angle DAT$ . Επίσης, $\angle DAS=arctan(\frac{x}{\frac{60}{13}})=arctan(\frac{13x}{60})$ και $\angle DCA=arctan(\frac{12}{5})\simeq 67,38$ . Άρα $\angle SAT=67,38-arctan(\frac{13x}{60})\Rightarrow \angle STA=90-67,38+arctan(\frac{13x}{60})=22,62+arctan(\frac{13x}{60})$ . Τέλος, από τον Νόμο των Ημιτόνων έχουμε πως $2R=AT=\frac{AS}{sin(\angle STA)}=\frac{\sqrt{x^2+\frac{3600}{169}}}{sin(22,62+arctan(\frac{13x}{60}))}$
Μέσα απο γραφικό κομπιουεράκι βρήκα πως η ελάχιστη τιμή του ΑΤ είναι περίπου 6.67

και επιτυγχάνεται όταν $x\simeq 3.077$ .
Β) Με ΠΘ βρίσκω πως $AD=\frac{b\cdot c}{a}=\frac{b\cdot c}{\sqrt{b^2+c^2}}$
Θέτω πάλι DS=x

και τώρα έχουμε από ΠΘ στο DAS πως $AS=\sqrt{AD^2+x^2}=\sqrt{\frac{b^2c^2}{b^2+c^2}+x^2}$ , $\angle ACB=\angle DAT=arctan(\frac{c}{b})$ (1), $\angle DAS=arctan(\frac{x}{\frac{bc}{\sqrt{b^2+c^2}}})=arctan(\frac{x\sqrt{(b^2+c^2)}}{bc})$ (2).
Από την αφαίρεση της (1) με την (2) προκύπτει:
$\angle SAT=arctan(\frac{c}{b})-arctan(\frac{x\sqrt{(b^2+c^2)}}{bc})$ .
Επομένως $\angle STA=90-\angle SAT=90-arctan(\frac{c}{b})+arctan(\frac{x\sqrt{(b^2+c^2)}}{bc})$ . Όπως και στο αποπάνω ερώτημα, από τον Νόμο των Ημιτόνων έχουμε πως $2R=AT=\frac{AS}{sin(\angle STA)}=\frac{\sqrt{x^2+\frac{b^2c^2}{b^2+c^2}}}{sin(90-arctan(\frac{c}{b})+arctan(\frac{x(\sqrt{b^2+c^2})}{bc}))}$ . Δηλαδή για να βρει κάποιος το ελάχιστο μήκος του ΑΤ αρκεί να βρει την ελάχιστη τιμή της παραπάνω συνάρτησης με περιορισμό φυσικά $0\leq DS=x\leq DB$
Γραφική παράσταση:https://www.desmos.com/calculator/drnaeebb12

#3

KARKAR έγραψε: ↑
Πέμ Μάιος 02, 2024 12:02 pm
Όσο πιο κοντά στην αρχή.pngΣτο ορθογώνιο τρίγωνο , με : , το είναι το ύψος προς την υποτείνουσα .

Σημείο κινείται στο εσωτερικό του τμήματος . Η κάθετη προς το τμήμα στο , τέμνει την ,

στο σημείο . Βρείτε το ελάχιστο μήκος του τμήματος . Γενίκευση για : .

Θεωρώ ορθογώνιο σύστημα συντεταγμένων με αρχή το

και οριζόντιο άξονα την ευθεία

. Τα σημεία A,B,C,D

θεωρούνται σταθερά.

Με δεδομένα μόνο τα $AB = c\,\,\kappa \alpha \iota \,\,AC = b\,\,\,\,\,\,(0 < b < c)$ προκύπτει εύκολα : $D\left( {\dfrac{{{b^2}c}}{{{a^2}}},\dfrac{{b{c^2}}}{{{a^2}}}} \right)\,\,,\,\,a = BC$ .

Το

διατρέχει το ευθύγραμμο τμήμα

. Αν η τετμημένη του

είναι $m\,\,$ θα είναι : $\dfrac{{{b^2}c}}{{{a^2}}} < m < c$ .

Οι συντεταγμένες του

προκύπτουν από τη λύση του συστήματος των εξισώσεων των ευθειών $AS\,\,\kappa \alpha \iota \,\,BC$ .

Αν λοιπόν $S\left( {m,k} \right)$ θα ισχύουν : $\left\{ \begin{gathered} y = \frac{{kx}}{m} \hfill \\ \frac{x}{c} + \frac{y}{b} = 1 \hfill \\ \end{gathered} \right.$ και προκύπτει : $S\left( {m,\dfrac{{b\left( {c - m} \right)}}{c}} \right)$ οπότε η ευθεία ,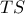

έχει εξίσωση , $\,y - \dfrac{{b\left( {c - m} \right)}}{c} = \dfrac{{mc\left( {x - m} \right)}}{{b\left( {m - c} \right)}}$ .

Για να προκύψει η τετμημένη ,

, του

, αρκεί να θέσω y = 0

κι έχω : $\boxed{AT = x = x\left( m \right) = \dfrac{{{b^2}{{\left( {c - m} \right)}^2} + {c^2}{m^2}}}{{c{m^2}}}}$ .

: Οσο πιο κοντά στην αρχή_ok.png (23.28 KiB) Προβλήθηκε 212 φορές

Με παραγώγους προκύπτει ότι το

γίνεται ελάχιστο όταν $\boxed{m = {m_0} = \dfrac{{bc}}{a}\,\,}$ και είναι : $\boxed{{x_{\min }} = \frac{{2b\left( {a - b} \right)}}{c}}$ .

Π.χ. με $b = 6\,\,\kappa \alpha \iota \,\,c = 8 \Rightarrow a = 10$ κι έχω για ${m_0} = \dfrac{{6 \cdot 8}}{{10}} = \dfrac{{24}}{5}$ ελάχιστο , ${x_{\min }} = \dfrac{{2 \cdot 6\left( {10 - 6} \right)}}{8} = 6$ . Τότε : $S\left( {\dfrac{{24}}{5},\dfrac{{12}}{5}} \right)$ .

Επίσης αν $b = 5\,\,,\,\,c = 12\,\, \Rightarrow c = 13\,\,,\,\,\boxed{S\left( {\dfrac{{60}}{{13}},\dfrac{{40}}{{13}}} \right)\,\,,\,\,A{T_{\min }} = \dfrac{{20}}{3}}$

#4

KARKAR έγραψε: ↑
Πέμ Μάιος 02, 2024 12:02 pm
Όσο πιο κοντά στην αρχή.pngΣτο ορθογώνιο τρίγωνο , με : , το είναι το ύψος προς την υποτείνουσα .

Σημείο κινείται στο εσωτερικό του τμήματος . Η κάθετη προς το τμήμα στο , τέμνει την ,

στο σημείο . Βρείτε το ελάχιστο μήκος του τμήματος . Γενίκευση για : .

Έστω

το μέσο του AT=2SM=2x.

Το ελάχιστο επιτυγχάνεται όταν το ημικύκλιο διαμέτρου

εφάπτεται της BC.

: Όσο πιο κοντά.Κ.png (16.77 KiB) Προβλήθηκε 203 φορές

$\displaystyle \frac{{SM}}{{AD}} = \frac{{CM}}{{CA}} \Leftrightarrow \frac{{ax}}{{bc}} = \frac{{b - x}}{b} \Leftrightarrow x = \frac{{bc}}{{a + c}} \Leftrightarrow$ $\boxed{A{T_{\min }} = \frac{{2bc}}{{a + c}}}$ όταν $\boxed{CS = \frac{{{b^2}}}{{a + c}}}$

Για την εφαρμογή c=5 , b=12, a=13,

είναι $\boxed{A{T_{\min }} = \frac{20}{3}}$ όταν $\boxed{CS=8}$

Κατά λάθος τα γράμματα μπήκαν ανάποδα απ' ό,τι στο σχήμα του θεματοδότη, οπότε τα τμήματα εναλλάσσονται με τα τμήματα της εκφώνησης.

Όσο πιο κοντά στην αρχή

Όσο πιο κοντά στην αρχή

Re: Όσο πιο κοντά στην αρχή

Re: Όσο πιο κοντά στην αρχή

Re: Όσο πιο κοντά στην αρχή

Μέλη σε σύνδεση