Παίρνω την πρωτοβουλία και προτείνω να κάνουμε εδώ μια συλλογή ασκήσεων
Αναλυτικής Γεωμετρίας, Διαφορικής Γεωμετρίας, Ευκλείδειας Γεωμετρίας, Ασκήσεων σε πολυπτύγματα κ.ο.κ.
Κάνω την αρχή με 5 ασκήσεις.
Άσκηση 1
Αν το διάνυσμα
 είναι κάθετο σε τρία μη συνεπίπεδα διανύσματα, τότε
είναι κάθετο σε τρία μη συνεπίπεδα διανύσματα, τότε  .
.Άσκηση 2
Μια πυραμίδα έχει κορυφές τα σημεία
 .
.Να βρείτε τον όγκο της και το ύψος από την κορυφή
 .
.Άσκηση 3 (Η ευθεία είναι ο συντομότερος δρόμος)
Έστω
 , όπου
, όπου  ένα ανοικτό διάστημα της πραγματικής ευθείας, μια λεία,
ένα ανοικτό διάστημα της πραγματικής ευθείας, μια λεία,κανονική παραμετρική καμπύλη. Έστω
![\displaystyle{\left[a,b\right]\subseteq I} \displaystyle{\left[a,b\right]\subseteq I}](/forum/ext/geomar/texintegr/latexrender/pictures/b706e32b8ceac291daf643af0f2daa81.png) . Θέτουμε
. Θέτουμε  .
.A. Δείξτε ότι για κάθε μοναδιαίο διάνυσμα
 ισχύει
ισχύει  .
.B. Δείξτε ότι

Άσκηση 4
Έστω
 μια κανονική παραμετρική καμπύλη. Υποθέτουμε ότι υπάρχει
μια κανονική παραμετρική καμπύλη. Υποθέτουμε ότι υπάρχει 
τέτοιο, ώστε η συνάρτηση
 να παρουσιάζει μέγιστο στο
να παρουσιάζει μέγιστο στο  .
.Αποδείξτε ότι
 , όπου
, όπου  είναι η καμπυλότητα της
είναι η καμπυλότητα της  .
.Άσκηση 5
Αποδείξτε ότι το δίχωνο υπερβολοειδές
 είναι μια κανονική επιφάνεια του
είναι μια κανονική επιφάνεια του  .
.
 (και γενικότερα τετραέδρου) δίδεται του τύπου:
(και γενικότερα τετραέδρου) δίδεται του τύπου:  .
.  είναι ίσο με
είναι ίσο με  .
. οπότε:
οπότε:

 τυχαίο διάνυσμα. Ας δηλώσουμε τα τρία μη συνεπίπεδα διανύσματα
τυχαίο διάνυσμα. Ας δηλώσουμε τα τρία μη συνεπίπεδα διανύσματα  αντίστοιχα . Επειδή είναι μη συνεπίπεδα θα 'ναι γραμμικώς ανεξάρτητα και επειδή είναι τρία το πλήθος θα αποτελούν μια βάση του
αντίστοιχα . Επειδή είναι μη συνεπίπεδα θα 'ναι γραμμικώς ανεξάρτητα και επειδή είναι τρία το πλήθος θα αποτελούν μια βάση του  . Έτσι , το τυχαίο διάνυσμα
. Έτσι , το τυχαίο διάνυσμα  θα γράφεται ως γραμμικώς συνδυασμός των
θα γράφεται ως γραμμικώς συνδυασμός των  όπου
όπου  πραγματικοί αριθμοί. Παίρνοντας εσωτερικό γινόμενο του
πραγματικοί αριθμοί. Παίρνοντας εσωτερικό γινόμενο του  και χρησιμοποιώντας τη γραμμικότητα του εσωτερικού γινομένου προκύπτει ότι το εσωτερικό γινόμενο του
και χρησιμοποιώντας τη γραμμικότητα του εσωτερικού γινομένου προκύπτει ότι το εσωτερικό γινόμενο του  . Άρα το
. Άρα το  έχουμε ότι
έχουμε ότι  άρα το μέτρο του
άρα το μέτρο του 
 .
.
 όπου η τελευταία είναι λόγω της γραμμικότητας του εσωτερικού γινομένου και η πρώτη ισότητα έπεται. Η δεύτερη ανισότητα είναι η ανισότητα
όπου η τελευταία είναι λόγω της γραμμικότητας του εσωτερικού γινομένου και η πρώτη ισότητα έπεται. Η δεύτερη ανισότητα είναι η ανισότητα  και το συμπέρασμα έπεται.
και το συμπέρασμα έπεται. και ας δηλώσουμε τη σχέση
και ας δηλώσουμε τη σχέση  .
.  το διάνυσμα
το διάνυσμα  το οποίο εύκολα ελέγχουμε ότι είναι μοναδιαίο. Τότε:
το οποίο εύκολα ελέγχουμε ότι είναι μοναδιαίο. Τότε:
 ανοιχτό διάστημα και
ανοιχτό διάστημα και  είναι λείες καμπύλες τότε ισχύει ότι
είναι λείες καμπύλες τότε ισχύει ότι  .
. .
. με τύπο
με τύπο  .
. είναι λείες στο
είναι λείες στο 
 και ισχύει ότι
και ισχύει ότι .
. είναι λεία απεικόνιση του
είναι λεία απεικόνιση του  ισχύει :
ισχύει :![\displaystyle{\begin{aligned} \dfrac{\mathrm{d}}{\mathrm{d}t}<f,g>(t)&=\dfrac{\mathrm{d}}{\mathrm{d}t}\,\left[\sum_{i=1}^{3}f_{i}(t)\,g_{i}(t)\right]\\&=\sum_{i=1}^{3}\dfrac{\mathrm{d}}{\mathrm{d}t}\left((f_{i}(t)\,g_{i}(t)\right)\\&=\sum_{i=1}^{3}\left[f_{i}^\prime(t)\,g_{i}(t)+f_{i}(t)\,g_{i}^\prime(t)\right]\\&=\sum_{i=1}^{3}f_{i}^\prime(t)\,g_{i}(t)+\sum_{i=1}^{3}f_{i}(t)\,g_{i}^\prime(t)\\&=<f^\prime(t),g(t)>+<f(t),g^\prime(t)>\end{aligned}} \displaystyle{\begin{aligned} \dfrac{\mathrm{d}}{\mathrm{d}t}<f,g>(t)&=\dfrac{\mathrm{d}}{\mathrm{d}t}\,\left[\sum_{i=1}^{3}f_{i}(t)\,g_{i}(t)\right]\\&=\sum_{i=1}^{3}\dfrac{\mathrm{d}}{\mathrm{d}t}\left((f_{i}(t)\,g_{i}(t)\right)\\&=\sum_{i=1}^{3}\left[f_{i}^\prime(t)\,g_{i}(t)+f_{i}(t)\,g_{i}^\prime(t)\right]\\&=\sum_{i=1}^{3}f_{i}^\prime(t)\,g_{i}(t)+\sum_{i=1}^{3}f_{i}(t)\,g_{i}^\prime(t)\\&=<f^\prime(t),g(t)>+<f(t),g^\prime(t)>\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/cc086c65f3df1655821d77774c609811.png)
 διανύσματα. Ας δειχθεί ότι:
διανύσματα. Ας δειχθεί ότι:
![\displaystyle{\left [ \vec{a} \times \vec{\beta}, \vec{\beta} \times \vec{\gamma} , \vec{\gamma} \times \vec{a} \right ]= \left [ \vec{a}, \vec{\beta}, \vec{\gamma} \right ]^2} \displaystyle{\left [ \vec{a} \times \vec{\beta}, \vec{\beta} \times \vec{\gamma} , \vec{\gamma} \times \vec{a} \right ]= \left [ \vec{a}, \vec{\beta}, \vec{\gamma} \right ]^2}](/forum/ext/geomar/texintegr/latexrender/pictures/27e6b2c41cebf9ae71cda845327a48b0.png)

 τυχούσα βάση διανυσματικού χώρου
τυχούσα βάση διανυσματικού χώρου  (όπου
(όπου  το
το  του Kronecker) ορίζουν μονοσήμαντα μία νέα τριάδα διανυσμάτων
του Kronecker) ορίζουν μονοσήμαντα μία νέα τριάδα διανυσμάτων  που δίδονται από τις σχέσεις:
που δίδονται από τις σχέσεις:

 .
. που οι αποστάσεις τους είναι όλες περιττοί ακέραιοι.
που οι αποστάσεις τους είναι όλες περιττοί ακέραιοι. με
με  .
. είναι λέια στον
είναι λέια στον  .
. . Για κάθε
. Για κάθε  ισχύει :
ισχύει :

 , αφού
, αφού  .
. είναι μια κανονική τιμή της
είναι μια κανονική τιμή της  είναι μια κανονική επιφάνεια του
είναι μια κανονική επιφάνεια του 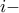 η συντεταγμένη. Έτσι έχω παραδείγματος χάρη:
η συντεταγμένη. Έτσι έχω παραδείγματος χάρη: 
 είναι ο τανυστής Levi-Civita. Tώρα παρατηρώ ότι
είναι ο τανυστής Levi-Civita. Tώρα παρατηρώ ότι  και χρησιμοποιώ την ταυτότητα
και χρησιμοποιώ την ταυτότητα

 . Προσθέτω κυκλικά και φτάνω στο ζητούμενο.
. Προσθέτω κυκλικά και φτάνω στο ζητούμενο.  είναι μια μη-μηδενιζόμενη και συνεχής πραγματική συνάρτηση , ορισμένη σε μια
είναι μια μη-μηδενιζόμενη και συνεχής πραγματική συνάρτηση , ορισμένη σε μια του
του  με
με  και
και  .
.
 και
και

 ,
, τότε
τότε 
 ,
, ,
, , πράγματι
, πράγματι 
 , που σημαίνει ότι το σημείο
, που σημαίνει ότι το σημείο , το οποίο έχει ρητές συντεταγμένες, είναι σημείο της καμπύλης
, το οποίο έχει ρητές συντεταγμένες, είναι σημείο της καμπύλης  .
. που διέρχονται από το σημείο
που διέρχονται από το σημείο  της
της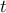 . Λύνουμε, για τυχόν
. Λύνουμε, για τυχόν  , το σύστημα των εξισώσεων της
, το σύστημα των εξισώσεων της στην εξόσωση της καμπύλης, βρίσκουμε
στην εξόσωση της καμπύλης, βρίσκουμε .
. , τότε
, τότε  (διπλή) και
(διπλή) και  (αναμενόμενο).
(αναμενόμενο). , τότε
, τότε  και
και  .
. με τύπους
με τύπους είναι τέτοιες, ώστε
είναι τέτοιες, ώστε  .
. .
. .
.
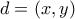 ,
,  ,
, ,
, 
 ,
,  άρα
άρα ,
, ,
, ,
, ,
,  ,
, ,
, ,
, 
 ώστε οι αποστάσεις τους να είναι όλες περιττοί ακέραιοι.
ώστε οι αποστάσεις τους να είναι όλες περιττοί ακέραιοι.  είναι
είναι  άρτιοι και οι δυο. Τότε ο αριθμός
άρτιοι και οι δυο. Τότε ο αριθμός  είναι περιττός (είναι ίσος με περιττός
είναι περιττός (είναι ίσος με περιττός  άρτιοι). Αντίστοιχα, ο αριθμός
άρτιοι). Αντίστοιχα, ο αριθμός  είναι περιττός.
είναι περιττός.  θα ήταν άρτιος, ως άθροισμα δυο περιττών και δυο άρτιων, άτοπο.
θα ήταν άρτιος, ως άθροισμα δυο περιττών και δυο άρτιων, άτοπο. είναι είτε και οι δυο άρτιοι είτε και οι δυο περιττοί, άρα και οι
είναι είτε και οι δυο άρτιοι είτε και οι δυο περιττοί, άρα και οι  είναι είτε και οι δυο άρτιοι είτε και οι δυο περιττοί. Σύμφωνα με το (α), αποκλείεται να είναι και οι δυο άρτιοι, άρα θα είναι και οι δυο περιττοί. Με τον ίδιο τρόπο, από την
είναι είτε και οι δυο άρτιοι είτε και οι δυο περιττοί. Σύμφωνα με το (α), αποκλείεται να είναι και οι δυο άρτιοι, άρα θα είναι και οι δυο περιττοί. Με τον ίδιο τρόπο, από την  είναι και οι δυο περιττοί. Επομένως
είναι και οι δυο περιττοί. Επομένως  θα είναι άρτιος ως άθροισμα τεσσάρων περιττών και δυο άρτιων, άτοπο.
θα είναι άρτιος ως άθροισμα τεσσάρων περιττών και δυο άρτιων, άτοπο. είναι άρτιος, διότι είτε είναι άθροισμα δυο άρτιων (αν
είναι άρτιος, διότι είτε είναι άθροισμα δυο άρτιων (αν  και
και  ή αντίστροφα), είτε είναι άθροισμα δυο περιττών (αν σε κάθε παρένθεση οι
ή αντίστροφα), είτε είναι άθροισμα δυο περιττών (αν σε κάθε παρένθεση οι  είναι διαφορετικής αρτιότητας). Αυτό συμπληρώνει την απόδειξη.
είναι διαφορετικής αρτιότητας). Αυτό συμπληρώνει την απόδειξη. ,
,  ,
,  (L. Piepmeyer. "The maximum number of odd integral distances between points in the plane ", Discrete & Computational Geometry January 1996, Volume 16, Issue 1, pp 113-115).
(L. Piepmeyer. "The maximum number of odd integral distances between points in the plane ", Discrete & Computational Geometry January 1996, Volume 16, Issue 1, pp 113-115). είναι εσωτερικό της γωνίας
είναι εσωτερικό της γωνίας  , από τα τρίγωνα
, από τα τρίγωνα  θα πάρουμε:
θα πάρουμε:



 και θα πάρουμε:
και θα πάρουμε: 





 είναι
είναι  (αφού ο
(αφού ο  είναι άρτιος ως γινόμενο διαδοχικών ακεραίων, άρα
είναι άρτιος ως γινόμενο διαδοχικών ακεραίων, άρα  .
. διότι είναι άθροισμα δυο τετραγώνων περιττών ακεραίων μείον ένα τετράγωνο περιττού ακεραίου (προφανώς και τα τετράγωνα των παρενθέσεων είναι
διότι είναι άθροισμα δυο τετραγώνων περιττών ακεραίων μείον ένα τετράγωνο περιττού ακεραίου (προφανώς και τα τετράγωνα των παρενθέσεων είναι  . Στο 2ο μέλος, ο πρώτος όρος είναι
. Στο 2ο μέλος, ο πρώτος όρος είναι  και ο δεύτερος όρος είναι
και ο δεύτερος όρος είναι  , άτοπο.
, άτοπο. στο
στο  ;
; στο
στο  .
. .
. ένα ευθύγραμμο τμήμα του επιπέδου και
ένα ευθύγραμμο τμήμα του επιπέδου και  και
και  ,
, είναι της μορφής
είναι της μορφής  όπου
όπου  . Τότε επειδή
. Τότε επειδή  συνάγουμε το συμπέρασμα πως η εξίσωση παριστάνει παραβολή.
συνάγουμε το συμπέρασμα πως η εξίσωση παριστάνει παραβολή. . Τότε επειδή
. Τότε επειδή  συνάγουμε ότι η εξίσωση αυτή είναι υπερβολή.
συνάγουμε ότι η εξίσωση αυτή είναι υπερβολή. έχουμε :
έχουμε :
 , που παρουσιάζει μέγιστο
, που παρουσιάζει μέγιστο το
το  .
. . Συνεπώς έχουμε μόνο μεταφορά:
. Συνεπώς έχουμε μόνο μεταφορά: . Οπότε θέτοντας
. Οπότε θέτοντας  η παραπάνω εξίσωση γράφεται:
η παραπάνω εξίσωση γράφεται:  που πράγματι είναι υπερβολή.
που πράγματι είναι υπερβολή. , οπότε
, οπότε  .
. 
 γίνεται ελάχιστο, ικανοποιείται η διαφορική Euler-Lagrange
γίνεται ελάχιστο, ικανοποιείται η διαφορική Euler-Lagrange  , οπότε θα έχουμε:
, οπότε θα έχουμε:  , με
, με 
 , δηλ.
, δηλ.  , άρα
, άρα  ( με
( με  κατάλληλη σταθερά).
κατάλληλη σταθερά).  (με
(με  σταθερά και
σταθερά και  επίσης σταθερά), άρα η γεωδαισιακή έχει παραμετρικές εξισώσεις
επίσης σταθερά), άρα η γεωδαισιακή έχει παραμετρικές εξισώσεις  .
.  και οι κύκλοι
και οι κύκλοι 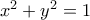 στα επίπεδα
στα επίπεδα  , όταν
, όταν  .
.