 είναι κορυφή ορθογωνίου τριγώνου
είναι κορυφή ορθογωνίου τριγώνου  , με τα άκρα της υποτείνουσας
, με τα άκρα της υποτείνουσας 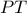 να είναι σημεία
να είναι σημείατου κύκλου :
 . Βρείτε την πιο απλή μορφή της εξίσωσης του γεωμ. τόπου του μέσου
. Βρείτε την πιο απλή μορφή της εξίσωσης του γεωμ. τόπου του μέσου  του
του 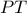 .
. είναι κορυφή ορθογωνίου τριγώνου
είναι κορυφή ορθογωνίου τριγώνου  , με τα άκρα της υποτείνουσας
, με τα άκρα της υποτείνουσας 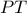 να είναι σημεία
να είναι σημεία . Βρείτε την πιο απλή μορφή της εξίσωσης του γεωμ. τόπου του μέσου
. Βρείτε την πιο απλή μορφή της εξίσωσης του γεωμ. τόπου του μέσου  του
του 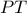 .
..
 του (σταθερού) τμήματος
του (σταθερού) τμήματος  (την ακτίνα το θα την δούμε στα παρακάτω).
(την ακτίνα το θα την δούμε στα παρακάτω).  . Έχουμε
. Έχουμε 

 , δίνει
, δίνει 
 είναι σταθερό, και ως μέσον του
είναι σταθερό, και ως μέσον του  έχει συντεταγμένες
έχει συντεταγμένες  , άρα το
, άρα το  κινείται επί κύκλου κέντρου
κινείται επί κύκλου κέντρου  . Συγκεκριμένα του
. Συγκεκριμένα του 
 και το
και το  είναι το
είναι το  . Σε αυτή την περίπτωση ο τόπος είναι ο
. Σε αυτή την περίπτωση ο τόπος είναι ο 
 , η οποία είναι απαλλαγμένη από κλάσματα .
, η οποία είναι απαλλαγμένη από κλάσματα ..
Την άσκηση( σε παραλλαγή) την είδαμε πριν περίπου 20 μέρες ως "Το τρίτο τμήμα 19" και στην Ευκλείδεια της έκφραση Εδώ
 βοηθάει πολύ στο να δεις το κέντρο και την ακτίνα του κύκλου
βοηθάει πολύ στο να δεις το κέντρο και την ακτίνα του κύκλου θα έχει κάποια αξία, δεν μπορεί!
θα έχει κάποια αξία, δεν μπορεί! ελέγχοντας το πρόσημο της διακρίνουσας
ελέγχοντας το πρόσημο της διακρίνουσας  .
.


Ίσως δεν έγινα κατανοητός. Κάνω άλλη μία προσπάθεια:
Πολύ ενδιαφέρον το ερώτημα, και ο Euler αυτό διαπραγματεύεται.
 που γράφει ο Euler είναι (το απρόσμενο) ότι περιλαμβάνει όλες τις κωνικές. Από εκεί και πέρα, για να μην εξετάζει κανείς κάθε φορά την διακρίνουσα
που γράφει ο Euler είναι (το απρόσμενο) ότι περιλαμβάνει όλες τις κωνικές. Από εκεί και πέρα, για να μην εξετάζει κανείς κάθε φορά την διακρίνουσα  για να αποφανθεί το είδος της κωνικής, οι ευκολότερες γραφές είναι προτιμητέες. Για παράδειγμα προτιμά κανείς την μορφή
για να αποφανθεί το είδος της κωνικής, οι ευκολότερες γραφές είναι προτιμητέες. Για παράδειγμα προτιμά κανείς την μορφή  της παραβολής, παρά την
της παραβολής, παρά την  . Ανάλογα, είναι πιο προσιτή η μορφή
. Ανάλογα, είναι πιο προσιτή η μορφή  μιας παραβολής, της οποίας αμέσως διακρίνει κανείς την μορφή και την κορυφή, παρά η ίδια στην μορφή
μιας παραβολής, της οποίας αμέσως διακρίνει κανείς την μορφή και την κορυφή, παρά η ίδια στην μορφή  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 0 επισκέπτες