 είναι σημείο του ημικυκλίου διαμέτρου
είναι σημείο του ημικυκλίου διαμέτρου  και η
και η  είναι η διχοτόμος της
είναι η διχοτόμος της  .
.Οι εφαπτόμενες του τόξου στα
 τέμνουν την προέκταση της
τέμνουν την προέκταση της  στα σημεία
στα σημεία  αντίστοιχα .
αντίστοιχα .Αν :
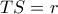 , εξετάστε αν είναι και :
, εξετάστε αν είναι και : 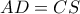 .
.Συντονιστής: gbaloglou
 είναι σημείο του ημικυκλίου διαμέτρου
είναι σημείο του ημικυκλίου διαμέτρου  και η
και η  είναι η διχοτόμος της
είναι η διχοτόμος της  .
. τέμνουν την προέκταση της
τέμνουν την προέκταση της  στα σημεία
στα σημεία  αντίστοιχα .
αντίστοιχα .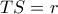 , εξετάστε αν είναι και :
, εξετάστε αν είναι και : 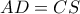 .
. ώστε να ισχύει η εν λόγω ισότητα.
ώστε να ισχύει η εν λόγω ισότητα.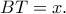 Είναι,
Είναι, 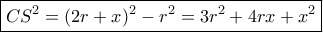
 Εξάλλου με νόμο συνημιτόνου στο
Εξάλλου με νόμο συνημιτόνου στο  έχω:
έχω: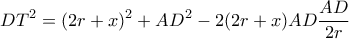 κι επειδή
κι επειδή 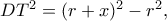
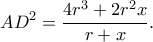 Αν τώρα είναι
Αν τώρα είναι 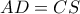 από την
από την  καταλήγω στην εξίσωση
καταλήγω στην εξίσωση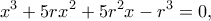 όπου με χρήση λογισμικού βρίσκω μοναδική λύση
όπου με χρήση λογισμικού βρίσκω μοναδική λύση 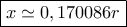
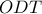 , είναι :
, είναι : 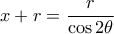 και από το
και από το 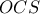 είναι :
είναι : 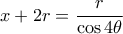 .
. καταλήγουμε ότι για την γωνία
καταλήγουμε ότι για την γωνία  , ισχύει :
, ισχύει : 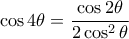 (*).
(*).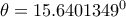 ) . Καλούμαστε λοιπόν
) . Καλούμαστε λοιπόν 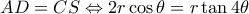
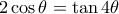 , η οποία ελέγχθηκε ( με λογισμικό) ότι ισχύει .
, η οποία ελέγχθηκε ( με λογισμικό) ότι ισχύει .Θανάση, παραπάνω όταν έγραφα ότι έχω λύση της άσκησης την οποία θα αναρτήσω, αυτήν ακριβώς την ακριβή απόδειξη είχα κατά νου. Δηλαδή την ισοδυναμία (με χρήση Τριγωνομετρίας, όχι λογισμικού)
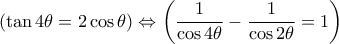
α) Έχουμε
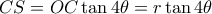 και
και 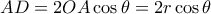 . Άρα η
. Άρα η 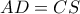 ισοδυναμεί με την
ισοδυναμεί με την 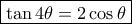
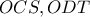 έχουμε
έχουμε 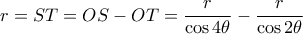 άρα
άρα 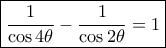
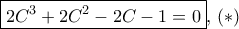 όπου
όπου 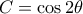 .
.  που δίνει την ισότητα των τμημάτων.
που δίνει την ισότητα των τμημάτων.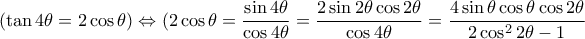 ισοδύναμα
ισοδύναμα 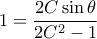 από όπου
από όπου 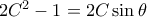 . Υψώνοντας στο τετράγωνο έχουμε
. Υψώνοντας στο τετράγωνο έχουμε 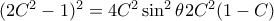 και άρα
και άρα 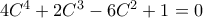 , ισοδύναμα
, ισοδύναμα 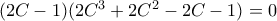 . Όμως
. Όμως 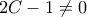 διότι δίνει
διότι δίνει  που απορρίπτεται γιατί το σχήμα απαιτεί
που απορρίπτεται γιατί το σχήμα απαιτεί 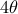 οξεία.
οξεία.  . Το βήμα αυτό αντιστρέφεται ακριβώς διότι
. Το βήμα αυτό αντιστρέφεται ακριβώς διότι 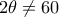 .
.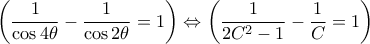 από όπου αμέσως η
από όπου αμέσως η  , και η απόδειξη ολοκληρώθηκε.
, και η απόδειξη ολοκληρώθηκε.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες