Τρίγωνο με καμπύλες

[mick7]

Το διάγραμμα δείχνει έναν κύκλο εγγεγραμμένο σε τρίγωνο Reuleaux. Αυτό το τρίγωνο, που πήρε το όνομά του από τον Γάλλο μηχανικό Franz Reuleaux (1829–1905), αποτελείται από τρία τόξα κύκλων με κέντρα στα σημεία A, B και 𝐶.
Κάθε ένας από αυτούς τους κύκλους έχει ακτίνα 6 εκ.

Ποια είναι η ακτίνα του εγγεγραμμένου κύκλου;

[george visvikis]

Το διάγραμμα δείχνει έναν κύκλο εγγεγραμμένο σε τρίγωνο Reuleaux. Αυτό το τρίγωνο, που πήρε το όνομά του από τον Γάλλο μηχανικό Franz Reuleaux (1829–1905), αποτελείται από τρία τόξα κύκλων με κέντρα στα σημεία A, B και 𝐶.
Κάθε ένας από αυτούς τους κύκλους έχει ακτίνα 6 εκ.

Ποια είναι η ακτίνα του εγγεγραμμένου κύκλου;

ΤΚ.png (19.75 KiB) Προβλήθηκε 2058 φορές

[mick7]

Βάζω και την λύση της άσκησης που είναι απο διαγωνισμό.

[KDORTSI]

Το διάγραμμα δείχνει έναν κύκλο εγγεγραμμένο σε τρίγωνο Reuleaux. Αυτό το τρίγωνο, που πήρε το όνομά του από τον Γάλλο μηχανικό Franz Reuleaux (1829–1905), αποτελείται από τρία τόξα κύκλων με κέντρα στα σημεία A, B και 𝐶.
Κάθε ένας από αυτούς τους κύκλους έχει ακτίνα 6 εκ.

Ποια είναι η ακτίνα του εγγεγραμμένου κύκλου;

Καλημέρα...

Το τρίγωνο του Reuleaux, όπως αναφέρεται στη μαθηματική ορολογία, από τα τέλη του 19ου αιώνα
αποτέλεσε μια ενδιαφέρουσα πρόκληση ακόμα και στη βιομηχανική του αξιοποίηση.
Σήμερα θεωρώ ότι μπορούμε και πάλι να ασχοληθούμε με το τρίγωνο αυτό έχοντας τη βοήθεια από
τις όμορφες απεικονιστικές μηχανές που διαθέτουμε.

Για το λόγο αυτό αναρτώ για όσους προκαλούνται από τέτοια θέματα την κύλιση του τριγώνου
αυτού μέσα σε ένα τετράγωνο. Στη δυναμική αυτή απεικόνιση λαμβάνεται υπόψη και ασφαλώς
διαπιστώνεται ότι, όπως ένα τέτοιο τρίγωνο μπορεί να κυλιστεί εντός μιας ζώνης παραλλήλων
ευθειών που απέχουν απόσταση ίση με τη διάμετρο του τριγώνου Reuleaux, έτσι αντίστοιχα
ένα τέτοιο τρίγωνο μπορεί να κυλιστεί και μέσα σε ένα τετράγωνο πλευράς ίσης με τη διάμετρο
του τριγώνου αυτού.

Αυτό φαίνεται στο ακόλουθο σχήμα:

Rouleaux 1.png (19.85 KiB) Προβλήθηκε 1871 φορές

Στο σχήμα αυτό η πλευρά του τετραγώνου θεωρήθηκε για απλούστευση ίση με:



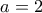
Οι τρεις κορυφές του τριγώνου διαγράφουν στις τέσσερις γωνίες του τετραγώνου

ελλειπτικά τόξα. Το κάτω αριστερά τόξο έχει παραμετρική εξίσωση:





όπου:



Για να δείτε την όλη κύλιση του τριγώνου αυτού αναρτώ
τον ακόλουθο σύνδεσμο:

https://www.geogebra.org/m/bybhemdh

Κώστας Δόρτσιος

[Al.Koutsouridis]

Και ένα παρεμφερές βίντεο στο πνέυμα της παραπάνω δημοσίευσης https://en.etudes.ru/etudes/drilling-square-holes/ .

[Ανδρέας Πούλος]

Αγαπητοί συνάδελφοι,
όλες οι αναρτήσεις που έγιναν με τίτλο "Τρίγωνο με καμπύλες" για το τρίγωνο του Reuleaux έχουν το ενδιαφέρον τους.
Θα ήθελα να σταθώ στην προσπάθεια που έκανε ο φίλος μου ο Κώστας Δόρτσιος να αναδείξει τη χρησιμότητα του λογισμικού Geogebra
στην κατασκευή της "τετράγωνης τρύπας" με περιστροφή του τριγώνου Reuleaux.
Το θέμα της κατασκευής της "τετράγωνης τρύπας" είχε απασχολήσει και τον Leonardo Da Vinci.
Με την ευκαιρία της ανάρτησης αυτής, υποβάλω μια εργασία που είχα δημοσιεύσει τον Μάρτιο του 2011 για το τρίγωνο Reuleaux
(ο οποίος αν και έχει γαλλικό επίθετο, ήταν Γερμανός). Βελτιωμένη εργασία για το ίδιο θέμα με πολλές διαφάνειες είχα παρουσιάσει
και σε μια ημερίδα του Σχολείου Καλαμαρί.

Το τρίγωνο του Ρελώ, Ανδρέας Πούλος.pdf

(844.83 KiB) Μεταφορτώθηκε 38 φορές

[mick7]

Προσθετω και εγώ αυτό με διάφορες προσομοιώσεις και μια κατασκευή ενός 'δρόμου' Reuleaux.

http://whistleralley.com/reuleaux/reuleaux.htm

[KDORTSI]

Προσθετω και εγώ αυτό με διάφορες προσομοιώσεις και μια κατασκευή ενός 'δρόμου' Reuleaux.

http://whistleralley.com/reuleaux/reuleaux.htm

Καλησπέρα...

Δοκίμασα κι εγώ τις δυνατότητες του Geogebra να παραστήσει έναν τέτοιο δρόμο, όπως
φαίνεται στο ακόλουθο σχήμα:

Κύλιση τριγώνου Reuleaux εντός ζώνης παραλλήλων ευθειών 1.png (8.39 KiB) Προβλήθηκε 1598 φορές

Μπορεί να το δει κανείς δυναμικά στη διεύθυνση:

https://www.geogebra.org/m/mukbkqrh

Κώστας Δόρτσιος