 (αντιμεταθετικού με μονάδα) που ικανοποιεί την ιδιότητα
(αντιμεταθετικού με μονάδα) που ικανοποιεί την ιδιότητα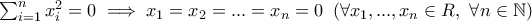
Μετά από μία (ομολογουμένως όχι επισταμένη) έρευνα στο internet, βρήκα παρεμφερείς έννοιες αλλά πουθενά αυτόν τον συγκεκριμένο ορισμό. Ξέρει κανείς την αγγλική/ελληνική απόδοση;
Ευχαριστώ πολύ!
Συντονιστής: Demetres
 (αντιμεταθετικού με μονάδα) που ικανοποιεί την ιδιότητα
(αντιμεταθετικού με μονάδα) που ικανοποιεί την ιδιότητα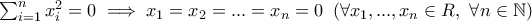
 , μαζί με τη συνηθισμένη με τα αλγεβρικά κλειστά σώματα (που δεν επιδέχονται γνήσια αλγεβρική επέκταση), όπως το
, μαζί με τη συνηθισμένη με τα αλγεβρικά κλειστά σώματα (που δεν επιδέχονται γνήσια αλγεβρική επέκταση), όπως το  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 0 επισκέπτες