Θεωρούμε ότι το

είναι εσωτερικό σημείο της πλευράς
 Ερώτημα A)
Ερώτημα A)
Όντας υποψιασμένοι από την (κεκρυμμένη) απάντηση του κυρίου Βισβίκη έχουμε:



Θέτουμε

και

και κατόπιν εφαρμόζουμε στον αριθμητή το πρώτο θέωρημα του Πτολεμαίου (
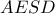
εγγράψιμο)




όπου

το ελάχιστο μέτρο της cevian


όταν

,

οξείες, το

είναι το ύψος του

από το

(όπως στην απάντηση του κυρίου Βισβίκη)

όταν

αμβλεία το

δεν έχει ελάχιστη τιμή αλλά infimum, την πλευρά


ομοίως όταν

αμβλεία το

έχει infimum, την πλευρά
 Ερώτημα B)
Ερώτημα B)
Αναγκαία συνθήκη για την παραλληλία

είναι τα
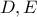
να βρίσκονται στην ίδια μεριά της ευθείας

οπότε αυτό αποκλείει το ενδεχόμενο οι γωνίες

του τριγώνου να είναι αμβλείες.
Ορθές επίσης δεν γίνεται να είναι γιατί όταν π.χ. η

είναι ορθή (οπότε

οξεία)
τότε

ενώ

οπότε

και έχουν κοινό σημείο το

οπότε είναι τεμνόμενες και συνεπώς όχι παράλληλες.
Θεωρώντας λοιπόν ότι οι

είναι οξείες, θα έχουμε:




και από το νόμο των συνημιτόνων βρίσκουμε τη μοναδική δυνατή τιμή του λόγου

για την οποία επιτυγχάνεται η ζητούμενη παραλληλία:

Επειδή οι

είναι οξείες το δεξί μέλος της τελευταίας είναι θετικό
Ο λόγος

για

μπορεί να λάβει οποιαδήποτε θετική τιμή
οπότε λαμβάνοντας τιμή ίση με το δεξί μέλος της τελευταίας ισότητας
λαμβάνουμε τη μοναδική θέση του

για την οποία επιτυγχάνεται η ζητούμενη παραλληλία

 κινείται στην βάση
κινείται στην βάση  τριγώνου
τριγώνου  . ( Στο παράδειγμα είναι :
. ( Στο παράδειγμα είναι :  .
. και
και  τέμνουν τις πλευρές
τέμνουν τις πλευρές 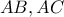 στα σημεία
στα σημεία  και
και  αντίστοιχα .
αντίστοιχα .  . Β) ( προς έρευνα ) Για ποια θέση του
. Β) ( προς έρευνα ) Για ποια θέση του  , προκύπτει :
, προκύπτει :  ;
;
 όταν το
όταν το  είναι ύψος.
είναι ύψος. 

 και
και 
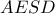 εγγράψιμο)
εγγράψιμο)



 το ελάχιστο μέτρο της cevian
το ελάχιστο μέτρο της cevian  όταν
όταν  ,
,  οξείες, το
οξείες, το  από το
από το 



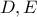 να βρίσκονται στην ίδια μεριά της ευθείας
να βρίσκονται στην ίδια μεριά της ευθείας  του τριγώνου να είναι αμβλείες.
του τριγώνου να είναι αμβλείες. ενώ
ενώ  οπότε
οπότε  και έχουν κοινό σημείο το
και έχουν κοινό σημείο το 




 είναι οξείες το δεξί μέλος της τελευταίας είναι θετικό
είναι οξείες το δεξί μέλος της τελευταίας είναι θετικό μπορεί να λάβει οποιαδήποτε θετική τιμή
μπορεί να λάβει οποιαδήποτε θετική τιμή 
 είναι το μέσο
είναι το μέσο  του
του 
 είναι σταθερή το ισοσκελές τρίγωνο
είναι σταθερή το ισοσκελές τρίγωνο  διατηρεί τις γωνίες του, άρα το
διατηρεί τις γωνίες του, άρα το 
 όταν
όταν 
 , καθιστά το μη υπολογιστικό μέρος της άσκησης σχετικά απλό .
, καθιστά το μη υπολογιστικό μέρος της άσκησης σχετικά απλό . είναι το ύψος. Πάμε τώρα στο υπολογιστικό κομμάτι.
είναι το ύψος. Πάμε τώρα στο υπολογιστικό κομμάτι. και από τα όμοια τρίγωνα
και από τα όμοια τρίγωνα  είναι
είναι 
 επιλύοντας το σύστημα:
επιλύοντας το σύστημα:
 με βάση τα στοιχεία του τριγώνου
με βάση τα στοιχεία του τριγώνου 
 ).
).