 είναι θετικοί ακέραιοι , να λυθεί το σύστημα:
είναι θετικοί ακέραιοι , να λυθεί το σύστημα:
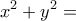 πολλ
πολλ
 είναι θετικοί ακέραιοι , να λυθεί το σύστημα:
είναι θετικοί ακέραιοι , να λυθεί το σύστημα:
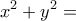 πολλ
πολλ
ΔΙΟΡΘΩΣΑ ένα τυπογραφικό: Αντί πολλ/σιο τουΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Πέμ Ιαν 19, 2023 4:05 pmΑνείναι θετικοί ακέραιοι , να λυθεί το σύστημα:
πολλ

 που είχα κατά λάθος γράψει, είναι πολλ/σιο του
που είχα κατά λάθος γράψει, είναι πολλ/σιο του  .
.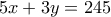
 πολ
πολ
Παρατηρούμε ότι τοΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Πέμ Ιαν 19, 2023 4:05 pmΑνείναι θετικοί ακέραιοι , να λυθεί το σύστημα:
πολλ

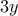 θα πρέπει να είναι πολλαπλάσιο του
θα πρέπει να είναι πολλαπλάσιο του  , άρα θα είναι πολλαπλάσιο του
, άρα θα είναι πολλαπλάσιο του  και το
και το  . Έστω ότι είναι της μορφής
. Έστω ότι είναι της μορφής 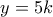 , όπου
, όπου  κάποιoς θετικός ακέραιος. Τότε η πρώτη εξίσωση του συστήματος γράφεται διαδοχικά
κάποιoς θετικός ακέραιος. Τότε η πρώτη εξίσωση του συστήματος γράφεται διαδοχικά
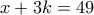

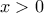 , θα είναι
, θα είναι 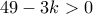 , δηλαδή
, δηλαδή  . Άρα για το
. Άρα για το 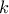 πρέπει να ισχύει
πρέπει να ισχύει  .
. που βρήκαμε στην πρώτη, έχουμε
που βρήκαμε στην πρώτη, έχουμε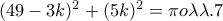




 θα πρέπει να είναι πολλαπλάσιο του
θα πρέπει να είναι πολλαπλάσιο του  και άρα και το
και άρα και το  . Οπότε οι δυνατές τιμές για το
. Οπότε οι δυνατές τιμές για το 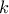 είναι
είναι  και
και  .
. έχουμε
έχουμε 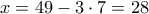 ,
, 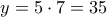
 έχουμε
έχουμε  ,
, 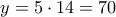 .
. , τότε ο καθένας εκ των αριθμών θα είναι πολλαπλάσιο του
, τότε ο καθένας εκ των αριθμών θα είναι πολλαπλάσιο του  (αφήνεται ως άσκηση). Χρησιμοποιώντας αυτό το αποτέλεσμα η πρώτη εξίσωση μπορεί να γραφεί στην μορφή
(αφήνεται ως άσκηση). Χρησιμοποιώντας αυτό το αποτέλεσμα η πρώτη εξίσωση μπορεί να γραφεί στην μορφή ή
ή
 . Από όπου βρίσκουμε ότι,
. Από όπου βρίσκουμε ότι, 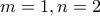 ή
ή  .
.Ας δούμε και μια εξήγηση, το γιατί αν το άθροισμα τετραγώνων δύο ακεραίων είναι πολλαπλάσιο τουAl.Koutsouridis έγραψε: ↑Κυρ Ιαν 22, 2023 12:27 pm
Εναλλακτικά θα μπορούσε κάποιος να δείξει ότι, αν το άθροισμα των τετραγώνων δυο αριθμών είναι πολλαπλάσιο του, τότε ο καθένας εκ των αριθμών θα είναι πολλαπλάσιο του
(αφήνεται ως άσκηση). Χρησιμοποιώντας αυτό το αποτέλεσμα η πρώτη εξίσωση μπορεί να γραφεί στην μορφή
ή

για κάποιους θετικούς ακέραιους. Από όπου βρίσκουμε ότι,
ή
.
 , τότε ο καθένας θα είναι επίσης πολλαπλάσιο του
, τότε ο καθένας θα είναι επίσης πολλαπλάσιο του 
 δεν είναι πολλαπλάσιo του
δεν είναι πολλαπλάσιo του  , τότε:
, τότε:


 δεν είναι πολλαπλάσιο του
δεν είναι πολλαπλάσιο του  , τότε ο
, τότε ο 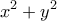 δεν θα ήταν
δεν θα ήταν , που αντίκειται στην υπόθεση.
, που αντίκειται στην υπόθεση.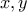 να είναι πολλαπλάσια του
να είναι πολλαπλάσια του  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης