
για τις οποίες ισχύει
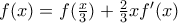
για κάθε

Συντονιστές: grigkost, Κοτρώνης Αναστάσιος

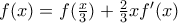

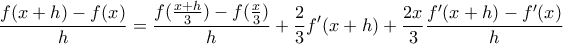
![\displaystyle \lim_{h \to 0} \left[ f'(x+h) + x\frac{f'(x+h) - f'(x)}{h}\right] = \frac{3}{2}f'(x) - \frac{1}{2}f'(\tfrac{x}{3}) \displaystyle \lim_{h \to 0} \left[ f'(x+h) + x\frac{f'(x+h) - f'(x)}{h}\right] = \frac{3}{2}f'(x) - \frac{1}{2}f'(\tfrac{x}{3})](/forum/ext/geomar/texintegr/latexrender/pictures/50218a12f1f8a293c0de37800cd8f95e.png)
 είναι συνεχής σε κάθε
είναι συνεχής σε κάθε  . Προφανώς είναι συνεχής στο
. Προφανώς είναι συνεχής στο  αφού τότε έχουμε
αφού τότε έχουμε 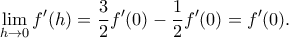 Έστω λοιπόν ότι δεν είναι συνεχής σε κάποιο
Έστω λοιπόν ότι δεν είναι συνεχής σε κάποιο  . Τότε υπάρχει
. Τότε υπάρχει  ώστε για κάθε
ώστε για κάθε  υπάρχει
υπάρχει  με
με  και
και 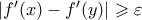 . Αλλά τότε από Darboux υπάρχει και
. Αλλά τότε από Darboux υπάρχει και 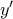 με
με  και
και 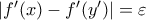 .
.  ώστε
ώστε 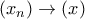 και
και  . Περνώντας σε μια υπακολουθία μπορούμε να υποθέσουμε ότι
. Περνώντας σε μια υπακολουθία μπορούμε να υποθέσουμε ότι 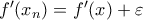 . Τότε όμως (για
. Τότε όμως (για  ) θα είχαμε ότι το
) θα είχαμε ότι το 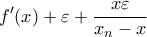 συγκλίνει όταν
συγκλίνει όταν  , άτοπο.
, άτοπο. και έστω
και έστω 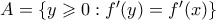 . Το
. Το  είναι μη κενό και κάτω φραγμένο οπότε έχει κάποιο infimum. Έστω
είναι μη κενό και κάτω φραγμένο οπότε έχει κάποιο infimum. Έστω 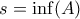 . Θα δείξουμε ότι
. Θα δείξουμε ότι  .
.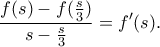
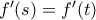 για κάποιο
για κάποιο 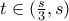 . Αυτό είναι άτοπο αφού τότε θα είχαμε και
. Αυτό είναι άτοπο αφού τότε θα είχαμε και  .
.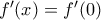 για κάθε
για κάθε  και ομοίως και για κάθε
και ομοίως και για κάθε  . Άρα η
. Άρα η  είναι σταθερή και η
είναι σταθερή και η  γραμμική.
γραμμική. Κάποιες παρατηρήσεις.Demetres έγραψε: ↑Πέμ Αύγ 22, 2019 7:45 pmΈχουμε:
Παίρνοντας όρια έχουμε:
Θα δείξουμε ότι ηείναι συνεχής σε κάθε
. Προφανώς είναι συνεχής στο
αφού τότε έχουμε
Έστω λοιπόν ότι δεν είναι συνεχής σε κάποιο
. Τότε υπάρχει
ώστε για κάθε
υπάρχει
με
και
. Αλλά τότε από Darboux υπάρχει και
με
και
.
Τότε όμως μπορούμε να βρούμε ακολουθίαώστε
και
. Περνώντας σε μια υπακολουθία μπορούμε να υποθέσουμε ότι
. Τότε όμως (για
) θα είχαμε ότι το
συγκλίνει όταν
, άτοπο.
Έστωκαι έστω
. Το
είναι μη κενό και κάτω φραγμένο οπότε έχει κάποιο infimum. Έστω
. Θα δείξουμε ότι
.
Έχουμε
Άρα από Θεώρημα Μέσης Τιμήςγια κάποιο
. Αυτό είναι άτοπο αφού τότε θα είχαμε και
.
Άραγια κάθε
και ομοίως και για κάθε
. Άρα η
είναι σταθερή και η
γραμμική.
Τέλος, παρατηρούμε ότι όλες οι γραμμικές συναρτήσεις ικανοποιούν τη συναρτησιακή.
Υ.Γ. Έγιναν κάποιες διορθώσεις.
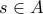 γιατί το
γιατί το  κλειστό.
κλειστό. συνεχής)
συνεχής) προκύπτει πολύ εύκολα ως εξής :
προκύπτει πολύ εύκολα ως εξής :
 (1)
(1) κάνουμε το εξής πιο απλό.
κάνουμε το εξής πιο απλό.
 .
. στον αριθμητή και χρησιμοποιώντας ότι το
στον αριθμητή και χρησιμοποιώντας ότι το υπάρχει.
υπάρχει. το όριο του αριστερού μέλους της (1)
το όριο του αριστερού μέλους της (1)  .
. είναι συνεχής στο
είναι συνεχής στο 
 . Για να μπορώ να πω ότι το
. Για να μπορώ να πω ότι το 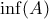 ανήκει στο
ανήκει στο  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 12 επισκέπτες