Στην τριάδα ακεραίων
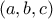 επενεργούμε το μετασχηματισμό
επενεργούμε το μετασχηματισμό  .
.Είναι δυνατόν να ξεκινήσουμε από την τριάδα
 και με διαδοχικούς μετασχηματισμούς να φτάσουμε σε μια κατάσταση
και με διαδοχικούς μετασχηματισμούς να φτάσουμε σε μια κατάσταση  , όπου ο ένας από τους
, όπου ο ένας από τους  αριθμούς είναι ίσος με το άθροισμα των άλλων
αριθμούς είναι ίσος με το άθροισμα των άλλων  ;
;Συντονιστής: Παύλος Μαραγκουδάκης
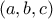 επενεργούμε το μετασχηματισμό
επενεργούμε το μετασχηματισμό  .
. και με διαδοχικούς μετασχηματισμούς να φτάσουμε σε μια κατάσταση
και με διαδοχικούς μετασχηματισμούς να φτάσουμε σε μια κατάσταση  , όπου ο ένας από τους
, όπου ο ένας από τους  αριθμούς είναι ίσος με το άθροισμα των άλλων
αριθμούς είναι ίσος με το άθροισμα των άλλων  ;
;Καλό.ksofsa έγραψε: ↑Τετ Δεκ 27, 2023 11:08 amΜε αφορμή το θέμα εδώ, προτείνω μια ιδιοκατασκευή:
Στην τριάδα ακεραίωνεπενεργούμε το μετασχηματισμό
.
Είναι δυνατόν να ξεκινήσουμε από την τριάδακαι με διαδοχικούς μετασχηματισμούς να φτάσουμε σε μια κατάσταση
, όπου ο ένας από τους
αριθμούς είναι ίσος με το άθροισμα των άλλων
;
 με τον αρχικό να είναι ο
με τον αρχικό να είναι ο  .
. τότε οι τρεις νέοι αριθμοί
τότε οι τρεις νέοι αριθμοί  διατηρούν την διάταξή τους καθώς (άμεσο)
διατηρούν την διάταξή τους καθώς (άμεσο)  .
.  ισχύει
ισχύει  . Συνεπώς
. Συνεπώς 



 μόνο που είναι δύο θέσεις νωρίτερα (την
μόνο που είναι δύο θέσεις νωρίτερα (την  φορά της επανάληψης αντί την
φορά της επανάληψης αντί την  ).
). είτε όταν
είτε όταν 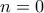 ή όταν
ή όταν  . Δηλαδή όταν η τριάδα ήταν η
. Δηλαδή όταν η τριάδα ήταν η  ή
ή  .
.  , οπότε η
, οπότε η  δεν ισχύει ποτέ.
δεν ισχύει ποτέ. ,
, κι ελάχιστο πολυώνυμο
κι ελάχιστο πολυώνυμο  .
. (από θεώρημα Cayley-Hamilton).
(από θεώρημα Cayley-Hamilton). .
. ή η τριάδα
ή η τριάδα  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης