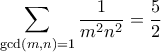 .
.Αθροίζοντας πάνω στους πρώτους
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
- Tolaso J Kos
- Δημοσιεύσεις: 5237
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Αθροίζοντας πάνω στους πρώτους
Να δειχθεί ότι 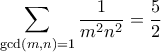 .
.
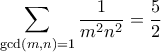 .
.Η φαντασία είναι σημαντικότερη από τη γνώση !


Λέξεις Κλειδιά:
- ΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ
- Δημοσιεύσεις: 921
- Εγγραφή: Πέμ Νοέμ 22, 2018 9:43 pm
Re: Αθροίζοντας πάνω στους πρώτους
Είναι
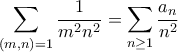 όπου
όπου  το πλήθος των διατεταγμένων ζευγών
το πλήθος των διατεταγμένων ζευγών  με
με 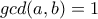 και
και  .
.Αν
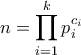 τότε είναι απλό να δούμε ότι
τότε είναι απλό να δούμε ότι 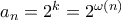
Οπότε θέλουμε να υπολογίσουμε το
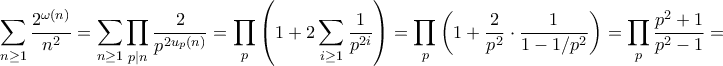
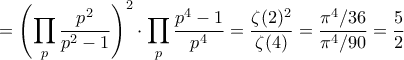
όπου
 συμβολίζει πάντα πρώτο.
συμβολίζει πάντα πρώτο.Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες
