 με
με  .
.Σημείωση: Έχω μια (σχεδόν) πλήρη λύση.
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
 με
με  .
.
α) Για
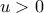 από το ΘΜΤ έχουμε
από το ΘΜΤ έχουμε 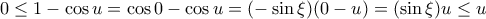 . Άρα για σταθερό
. Άρα για σταθερό  έχουμε
έχουμε 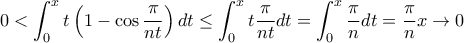
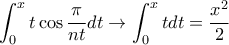
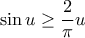 για
για  στο πρώτο τετρατημόριο (η ανίσωση είναι γνωστή, και βγαίνει εύκολα δείχνοντας πρώτα ότι η
στο πρώτο τετρατημόριο (η ανίσωση είναι γνωστή, και βγαίνει εύκολα δείχνοντας πρώτα ότι η 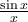 είναι φθίνουσα) έχουμε ολοκληρώνοντας (πάντα για
είναι φθίνουσα) έχουμε ολοκληρώνοντας (πάντα για  στο πρώτο τεταρτημόριο) ότι
στο πρώτο τεταρτημόριο) ότι 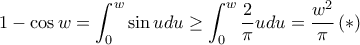 .
. 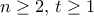 το
το 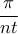 είναι στο πρώτο τεταρτημόριο έχουμε για
είναι στο πρώτο τεταρτημόριο έχουμε για  ότι
ότι 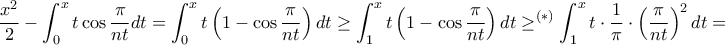
 που για
που για  ισούται με
ισούται με  , πάντως δεν τείνει στο
, πάντως δεν τείνει στο 
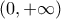 απέχει πολύ από την κομψή λύση του κ. Λάμπρου, μιας και περιλαμβάνει τις συναρτήσεις
απέχει πολύ από την κομψή λύση του κ. Λάμπρου, μιας και περιλαμβάνει τις συναρτήσεις  και
και  , (μαζί με ένα αναπόδεικτο όριο). Επομένως δεν προσθέτει δημιουργικά.
, (μαζί με ένα αναπόδεικτο όριο). Επομένως δεν προσθέτει δημιουργικά.![({0,\pi}] ({0,\pi}]](/forum/ext/geomar/texintegr/latexrender/pictures/7df5edf7c71203597ee0e3db7970245a.png) ή σε οποιοδήποτε διάστημα της μορφή
ή σε οποιοδήποτε διάστημα της μορφή ![({0,a}] ({0,a}]](/forum/ext/geomar/texintegr/latexrender/pictures/43640895cd281af37f84b3cbe0aa5708.png) , για σταθερό
, για σταθερό  ,
,
Ναι, συγκλίνει ομοιόμορφα:
 για
για  έχουμε για
έχουμε για  στο φραγμένο διάστημα
στο φραγμένο διάστημα ![[0,a] [0,a]](/forum/ext/geomar/texintegr/latexrender/pictures/13596d6674a86fdafa24c4c414033e58.png) ότι
ότι 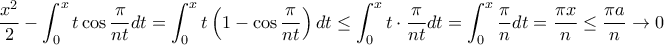
 ).
).Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 16 επισκέπτες