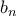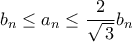Δύο ακολουθίες
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
-
orestisgotsis
- Δημοσιεύσεις: 1753
- Εγγραφή: Σάβ Φεβ 25, 2012 10:19 pm
Δύο ακολουθίες
ΠΕΡΙΤΤΑ
τελευταία επεξεργασία από orestisgotsis σε Παρ Φεβ 23, 2024 2:21 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Λέξεις Κλειδιά:
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15768
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Δύο ακολουθίες
(1) Mε άμεση αντιπαράγωγο,orestisgotsis έγραψε: ↑Σάβ Ιαν 27, 2024 7:00 pmΔίνονται οι ακολουθίεςόπου:
και
.
(1) Υπολογίστε τον
(2) Αποδείξτε ότι για κάθε,
(3) Υπολογίστε το.
![b_n= \left [\dfrac {1}{n} e^{n\sin x} \right ]_{-\pi /6}^{\pi /6} = \dfrac {1}{n} \left (e^{n/2} - e^{-n/2} \right ) b_n= \left [\dfrac {1}{n} e^{n\sin x} \right ]_{-\pi /6}^{\pi /6} = \dfrac {1}{n} \left (e^{n/2} - e^{-n/2} \right )](/forum/ext/geomar/texintegr/latexrender/pictures/b64810af8a1b4d1985f2b13b8699fd8c.png)
(2) Επειδή στο διάστημα
![\left [-\frac{\pi }{6},\, \frac{\pi }{6} \right ] \left [-\frac{\pi }{6},\, \frac{\pi }{6} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/f1f35f45218e2a92a9376f084a65c09d.png) ισχύει
ισχύει 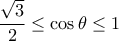 έχουμε
έχουμε 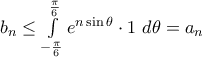 και
και 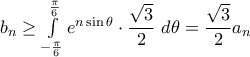
από όπου τα ζητούμενα.
(3)
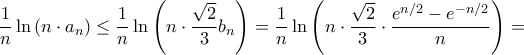
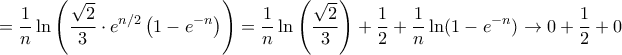
Και όμοια
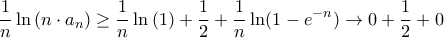
Από ισοσυγκλίνουσες, το ζητούμενο όριο είναι

Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες