Όριο με αρμονικά

Tolaso J Kos · #1

Έστω $\mathcal{H}_n$ ο

- οστός αρμονικός όρος. Να υπολογιστεί το όριο:

$\displaystyle{\ell = \lim_{n \rightarrow +\infty} \left ( \mathcal{H}_n - \frac{1}{n} \sum_{k=1}^{n} \mathcal{H}_k \right )}$
Αυτή η δημοσίευση θα ναι και η τελευταία μου για το καλοκαίρι. Θα παρακολουθώ το ως επισκέπτης αλλά δυστυχώς επαγγελματικές μου δραστηριότητες δε μου αφήνουν πολύ χρόνο να ασχολούμαι με το αν και έχω αρκετό υλικό. Θα επιστρέψω πάλι δριμύτερος στο μέλλον.

#2

Tolaso J Kos έγραψε: ↑
Τρί Αύγ 11, 2020 3:50 pm
Έστω $\mathcal{H}_n$ ο - οστός αρμονικός όρος. Να υπολογιστεί το όριο:

$\displaystyle{\ell = \lim_{n \rightarrow +\infty} \left ( \mathcal{H}_n - \frac{1}{n} \sum_{k=1}^{n} \mathcal{H}_k \right )}$

Από Cesaro και από τον ορισμό της σταθεράς Euler–Mascheroni έχουμε ότι το αριστερό μέλος ισούται

$\displaystyle{ \left ( \mathcal{H}_n -\ln n \right ) - \frac{1}{n} \sum_{k=1}^{n} \left ( \mathcal{H}_k -\ln k \right )+ \ln n - \frac{1}{n} \ln n!}$

Οι δύο πρώτοι όροι τείνουν στο $\gamma -\gamma =0$ , οπότε μένει να βρούμε το όριο της $\displaystyle{\ln n - \frac{1}{n} \ln n!}$ . Μας το δίνει εύκολα ο τύπος του Stirling, $\displaystyle{\ln n!= n\ln n -n +O(\ln n)}$ , από όπου το όριο είναι

.

Tolaso J Kos · #3

Να το συνεχίσουμε λίγο; Αν και δεν χρειάστηκε κάπου ας δειχθεί ότι:

$\displaystyle{\sum_{k=1}^{n} \mathcal{H}_k = \left ( n + 1 \right ) \left ( \mathcal{H}_{n+1} - 1 \right )}$
Καλή συνέχεια σε όλα τα μέλη του . Εις το επανιδείν.

#4

Tolaso J Kos έγραψε: ↑
Τρί Αύγ 11, 2020 5:47 pm
Να το συνεχίσουμε λίγο; Αν και δεν χρειάστηκε κάπου ας δειχθεί ότι:

$\displaystyle{\sum_{k=1}^{n} \mathcal{H}_k = \left ( n + 1 \right ) \left ( \mathcal{H}_{n+1} - 1 \right )}$

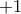Ας κάνουμε δύο πράγματα: α) Την απόδειξη του παραπάνω και β) λύση της αρχικής άσκησης με χρήση αυτού (που είναι αρκετά απλούστερο, αφού γλυτώνομε την σταθερά Euler-Mascheroni και τον τύπο του Stirling).

α) Με επαγωγή: Για το επαγωγικό βήμα αφού ελέγξουμε την περίπτωση n=1

(άμεσο), έχουμε

$\displaystyle{\displaystyle{\sum_{k=1}^{n+1} \mathcal{H}_k = \sum_{k=1}^{n+1} \mathcal{H}_k + \mathcal{H}_{n+1} = \left ( n + 1 \right ) \left ( \mathcal{H}_{n+1} - 1 \right )+ \mathcal{H}_{n+1}= (n+2) \mathcal{H}_{n+1} - (n+1)}$

$\displaystyle{ (n+2)\left ( \mathcal{H}_{n+2}- \dfrac {1}{n+2} \right ) - (n+1) = (n+2) \mathcal{H}_{n+2} -1- (n+1)= (n+2)\left ( \mathcal{H}_{n+2}-1 \right ) }$ , όπως θέλαμε.

β) $\displaystyle{ \displaystyle{ \mathcal{H}_n - \frac{1}{n} \sum_{k=1}^{n} \mathcal{H}_k }=\mathcal{H}_n -\dfrac {n+1}{n} \left ( \mathcal{H}_{n+1} - 1 \right )} = \mathcal{H}_n -\dfrac {n+1}{n} \left ( \mathcal{H}_{n} + \dfrac {1}{n+1}- 1 \right )= } }$

$\displaystyle{ = -\dfrac {1}{n} \mathcal{H}_{n} +1 \rightarrow 1}$ διότι $\displaystyle{\dfrac {1}{n} \mathcal{H}_{n}\sim \dfrac {\ln n}{n}\rightarrow 0}$

Όριο με αρμονικά

Όριο με αρμονικά

Re: Όριο με αρμονικά

Re: Όριο με αρμονικά

Re: Όριο με αρμονικά

Μέλη σε σύνδεση