 ,
, 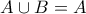 τότε ,
τότε , είναι το κενό σύνολο
είναι το κενό σύνολοΑς υποθέσουμε ότι
 δεν είναι κενό τότε υπάρχει χ και
δεν είναι κενό τότε υπάρχει χ και 
Αλλά δεν μπορώ να φτάσω σε μία αντίφαση
 ; (Το edit για συντακτικό.)
; (Το edit για συντακτικό.)Η άσκηση είναι απλούστατη.
 ίσον το κενό σύνολο και δες τι σου δίνει η υπόθεση. (Προσθήκη αργότερα: Τώρα διαπίστωσα ότι ουσιαστικά αυτό σου λέει ο llenny παραπάνω).
ίσον το κενό σύνολο και δες τι σου δίνει η υπόθεση. (Προσθήκη αργότερα: Τώρα διαπίστωσα ότι ουσιαστικά αυτό σου λέει ο llenny παραπάνω). . Πάρε και ένα
. Πάρε και ένα 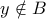 . Εξέτασε τώρα το σύνολο
. Εξέτασε τώρα το σύνολο 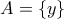 .
.Μα έαν πάρωMihalis_Lambrou έγραψε: ↑Κυρ Δεκ 20, 2020 11:37 pmΗ άσκηση είναι απλούστατη.
Υπόδειξη για πρώτη λύση: Πάρείσον το κενό σύνολο και δες τι σου δίνει η υπόθεση. (Προσθήκη αργότερα: Τώρα διαπίστωσα ότι ουσιαστικά αυτό σου λέει η llenny παραπάνω).
Υπόδειξη για δεύτερη λύση με βάση το ξεκίνημα που έκανες: Πήρες λοιπόν. Πάρε και ένα
. Εξέτασε τώρα το σύνολο
.
Θα χαρούμε να δούμε εδώ την λύση σου.
 Aυτόματα έχουμε μια αντίφαση
Aυτόματα έχουμε μια αντίφαση 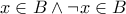 και από μια αντίφαση μπορούμε να συμπεράνουμε οτιδήποτε,δηλαδή
και από μια αντίφαση μπορούμε να συμπεράνουμε οτιδήποτε,δηλαδή 
 {
{  }
}  {
{ }
}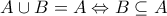
Δεν είναι αντιπαράδειγμα στο αρχικό σου πρόβλημα (στο πρώτο ποστ). Χρησιμοποίησες ένα
 και όχι όλα όπως λέει η εκφώνηση.
και όχι όλα όπως λέει η εκφώνηση.  διάφορο του κενού για το οποίο ισχύει η υπόθεση ΓΙΑ ΚΑΘΕ
διάφορο του κενού για το οποίο ισχύει η υπόθεση ΓΙΑ ΚΑΘΕ  . Δεν έκανες κάτι τέτοιο.
. Δεν έκανες κάτι τέτοιο.  , αλλά μόνο του
, αλλά μόνο του  .
.Επειδή έχω πρόβλημα με τις αγκύλες και το Latex θα γράψω το αντιπαράδειγμα χωρίς Latex.Mihalis_Lambrou έγραψε: ↑Δευ Δεκ 21, 2020 8:24 amΑν επρόκειτο για αντιπαράδειμα θα έπρεπε να έδινες έναδιάφορο του κενού για το οποίο ισχύει η υπόθεση
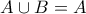 είναι ισοδύναμο με
είναι ισοδύναμο με 
.labrosb έγραψε: ↑Δευ Δεκ 21, 2020 5:23 pm
Επειδή έχω πρόβλημα με τις αγκύλες και το Latex θα γράψω το αντιπαράδειγμα χωρίς Latex.
Β δεν είναι κενό αλλά
Β={1}
Αλλο αντιπαράδειγμα:
Α={1,2,3,4}...................................Β={2,3}
Α={1,2,3}.....................................Β={1,2}
Α={1}...........................................Β={1} κ.τ.λ
Εξάλλουείναι ισοδύναμο με

 διάφορο του κενού για το οποίο ισχύει η υπόθεση ΓΙΑ ΚΑΘΕ
διάφορο του κενού για το οποίο ισχύει η υπόθεση ΓΙΑ ΚΑΘΕ  . Δεν έκανες κάτι τέτοιο. Για αντιπαράδειγμα ΔΕΝ ΕΧΕΙΣ επλογή του
. Δεν έκανες κάτι τέτοιο. Για αντιπαράδειγμα ΔΕΝ ΕΧΕΙΣ επλογή του  , αλλά μόνο του
, αλλά μόνο του  .
. για το εκάστοτε
για το εκάστοτε  . Όμως η άσκσηση λέει ότι πρέπει να ισχύει
. Όμως η άσκσηση λέει ότι πρέπει να ισχύει 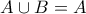 για κάθε
για κάθε  . Με άλλα λόγια, χειριζόμενος το σωστό
. Με άλλα λόγια, χειριζόμενος το σωστό  θα βγάλεις το ζητούμενο αποδεικτέο. Όλα τα παραδείγματα που δίνεις απλά λένε ότι το
θα βγάλεις το ζητούμενο αποδεικτέο. Όλα τα παραδείγματα που δίνεις απλά λένε ότι το  που επέλεξες ΔΕΝ ΕΙΝΑΙ ΤΟ ΚΑΤΑΛΛΗΛΟ για το αποδεικτέο.
που επέλεξες ΔΕΝ ΕΙΝΑΙ ΤΟ ΚΑΤΑΛΛΗΛΟ για το αποδεικτέο. 
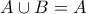 . Άν όμως έπαιρνες
. Άν όμως έπαιρνες  τότε θα είχαμε
τότε θα είχαμε 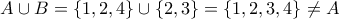
 σου ΔΕΝ ΙΚΑΝΟΠΟΙΕΙ τις προϋποθέσεις της άσκησης οπότε ΔΕΝ ΕΙΝΑΙ ΑΝΤΙΠΑΡΑΔΕΙΓΜΑ στην άσκηση.
σου ΔΕΝ ΙΚΑΝΟΠΟΙΕΙ τις προϋποθέσεις της άσκησης οπότε ΔΕΝ ΕΙΝΑΙ ΑΝΤΙΠΑΡΑΔΕΙΓΜΑ στην άσκηση. ισχύει
ισχύει 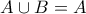 , τότε
, τότε 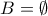 .
. αυτό και για κάθε
αυτό και για κάθε  ισχύει
ισχύει  ........ (το
........ (το  ισχύει για όλα τα σύνολα, το
ισχύει για όλα τα σύνολα, το  είναι η υπόθεσή μας.)
είναι η υπόθεσή μας.) ειναι υποσύνολο κάθε συνόλου. Άρα το
ειναι υποσύνολο κάθε συνόλου. Άρα το  είναι το κενό: Αυτό είναι άμεσο αλλά αν θέλουμε να το δούμε χειροποιαστά, μπορούμε να εφαρμόσουμε το συμπέρασμά μας στο
είναι το κενό: Αυτό είναι άμεσο αλλά αν θέλουμε να το δούμε χειροποιαστά, μπορούμε να εφαρμόσουμε το συμπέρασμά μας στο 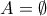 , οπότε
, οπότε 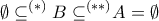 ........ (το
........ (το  ισχύει για όλα τα σύνολα, το
ισχύει για όλα τα σύνολα, το  ισχύει από αυτό που δείξαμε.)
ισχύει από αυτό που δείξαμε.)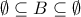
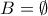 , όπως θέλαμε.
, όπως θέλαμε.Ο Συγγραφέας διατυπώνει στην σελίδα 17 το :Mihalis_Lambrou έγραψε: ↑Δευ Δεκ 21, 2020 6:24 pm.labrosb έγραψε: ↑Δευ Δεκ 21, 2020 5:23 pm
Επειδή έχω πρόβλημα με τις αγκύλες και το Latex θα γράψω το αντιπαράδειγμα χωρίς Latex.
Β δεν είναι κενό αλλά
Β={1}
Αλλο αντιπαράδειγμα:
Α={1,2,3,4}...................................Β={2,3}
Α={1,2,3}.....................................Β={1,2}
Α={1}...........................................Β={1} κ.τ.λ
Εξάλλουείναι ισοδύναμο με

Πάλι τα ίδια. Κάνω άλλη μία προσπάθεια.
Αν επρόκειτο για αντιπαράδειμα θα έπρεπε να έδινες έναδιάφορο του κενού για το οποίο ισχύει η υπόθεση ΓΙΑ ΚΑΘΕ
. Δεν έκανες κάτι τέτοιο. Για αντιπαράδειγμα ΔΕΝ ΕΧΕΙΣ επλογή του
, αλλά μόνο του
.
Σε όλα τα παραδείγματα επιλέγεις κάποιογια το εκάστοτε
. Όμως η άσκσηση λέει ότι πρέπει να ισχύει
για κάθε
. Με άλλα λόγια, χειριζόμενος το σωστό
θα βγάλεις το ζητούμενο αποδεικτέο. Όλα τα παραδείγματα που δίνεις απλά λένε ότι το
που επέλεξες ΔΕΝ ΕΙΝΑΙ ΤΟ ΚΑΤΑΛΛΗΛΟ για το αποδεικτέο.
Ας δούμε ένα παράδειγμα ώστε να καταλάβουμε γιατί αυτά που γράφεις δεν λειτουργούν. Έχεις πάρει για παράδειγμα

Εδώ πράγματι ισχύει. Άν όμως έπαιρνες
τότε θα είχαμε
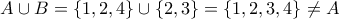
Δηλαδή τοσου ΔΕΝ ΙΚΑΝΟΠΟΙΕΙ τις προϋποθέσεις της άσκησης οπότε ΔΕΝ ΕΙΝΑΙ ΑΝΤΙΠΑΡΑΔΕΙΓΜΑ στην άσκηση.
Και για να κλείνω δίνω απόδειξη του αποδεικτέου, αν και είναι τόσο απλό που δεν ξέρω γιατί κολλάμε. Ζητώ συγνώμη από τους αναγνώστες, αλλά θα είμαι κάπως αναλυτικός για την αξία της άσκησης.
Προς αποφυγήν παρεξηγήσεων, θέλουμε να δείξουμε ότι αν για κάθεισχύει
, τότε
.
Απόδειξη: Για τοαυτό και για κάθε
ισχύει
........ (το
ισχύει για όλα τα σύνολα, το
είναι η υπόθεσή μας.)
Δηλαδή δείξαμε ότι τοειναι υποσύνολο κάθε συνόλου. Άρα το
είναι το κενό: Αυτό είναι άμεσο αλλά αν θέλουμε να το δούμε χειροποιαστά, μπορούμε να εφαρμόσουμε το συμπέρασμά μας στο
, οπότε
........ (το
ισχύει για όλα τα σύνολα, το
ισχύει από αυτό που δείξαμε.)
Δηλαδή
Άρα, εξ ορισμού,, όπως θέλαμε.
Κλείνω προσθέτοντας ότι υπάρχουν και άλλες αποδείξεις του ιδίου, εξ ίσου απλές.
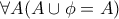 Αυτό είναι ισοδύναμο με :
Αυτό είναι ισοδύναμο με : ![\exists B\forall A[A\cup B=A] \exists B\forall A[A\cup B=A]](/forum/ext/geomar/texintegr/latexrender/pictures/dd76b970b277672a34eaa4f05f827317.png)
![[\exists B\forall A(A\cup B=A)]\Rightarrow B=\phi [\exists B\forall A(A\cup B=A)]\Rightarrow B=\phi](/forum/ext/geomar/texintegr/latexrender/pictures/7fe86abeda2f23f1e4fffdb76926578b.png) ΚΑΙ δεν χρειάζεται ούτε καν απόδειξη
ΚΑΙ δεν χρειάζεται ούτε καν απόδειξη![[\exists B\forall A(A\cup B=A)]\Rightarrow B=\phi [\exists B\forall A(A\cup B=A)]\Rightarrow B=\phi](/forum/ext/geomar/texintegr/latexrender/pictures/7fe86abeda2f23f1e4fffdb76926578b.png)
Τώρα είναι που με μπέρδεψες τελείως.
Νόμισα ότι ο συγγραφέας ζητούσε να αποδείξουμε:Mihalis_Lambrou έγραψε: ↑Δευ Δεκ 21, 2020 10:42 pmΤώρα είναι που με μπέρδεψες τελείως.
Τόσην ώρα έλεγες ότι δεν ισχύει το αποτέλεσμα και μας έδινες αντιπαραδείγματα (τρόπος του λέγειν) ότι είναι εσφαλμένο. Ξαφνικά λες ότι ισχύει το αποτέλεσμα και ότι είναι τόσο απλό που δεν χρειάζεται απόδειξη. Άσε που στο πρώτο ποστ δηλώνεις, αντίθετα, αδυναμία να αποδείξεις το ζητούμενο.
Το ότι είναι πάρα πολύ απλό το αποτέλεσμα, το ξέρω και το έχω πει τόσες φορές. Αφού απολογούμαι στους αναγνώστες που γράφω αναλυτικά μία τόσο απλή απόδειξη. Άλλωστε καταλήγω στο ότι υπάρχουν και άλλες αποδείξεις, εξ ίσου απλές. Προς τι λοιπόν τόση φασαρία και ερώτημα αν συμφωνώ; Προς τι να συμφωνήσω; Στο ότι το θέμα είναι απλούστατο; Συμφωνώ!
Εσύ συμφωνείς ότι τα "αντιπαραδείγματά" σου ήταν λάθος;
![\forall A\forall B[A\cup B=A\Leftrightarrow B=0] \forall A\forall B[A\cup B=A\Leftrightarrow B=0]](/forum/ext/geomar/texintegr/latexrender/pictures/4c1c469f4ff53981afadd6625f2672c7.png) για αυτό και τα λάθος αντιπαραδείγματα ,ενώ ο συγγραφέας ζητούσε λανθασμένα
για αυτό και τα λάθος αντιπαραδείγματα ,ενώ ο συγγραφέας ζητούσε λανθασμένα ![\forall A[A\cup B\Rightarrow B=0] \forall A[A\cup B\Rightarrow B=0]](/forum/ext/geomar/texintegr/latexrender/pictures/2ffd71ffb65c48f9268f0926fbbfbfe0.png) .Εδώ έχουμε μια μεταβλητή Β για την οποία δεν υπάρχει ποσοδείκτης πράγμα που οδηγεί σε λανθασμένες ερμηνείες
.Εδώ έχουμε μια μεταβλητή Β για την οποία δεν υπάρχει ποσοδείκτης πράγμα που οδηγεί σε λανθασμένες ερμηνείες τέτοιο ώστε για όλα τα
τέτοιο ώστε για όλα τα  ,
,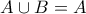 τότε
τότε 
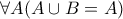 Βάλε
Βάλε  Και έχουμε
Και έχουμε 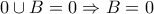
Σωστά. Αν προσέξεις, αυτήν ακριβώς την απόδειξη έγραψα εκτός από το γεγονός ότι ήμουν αναλυτικός σε υπερθετικό βαθμό.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες