31. Αν
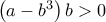 , τότε ο
, τότε ο 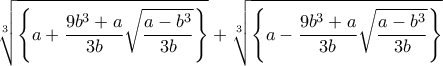
είναι ρητός
[ Κάθε ένας από τους αριθμούς κάτω από την κυβική ρίζα είναι της μορφής
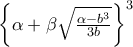 , όπου οι
, όπου οι  και
και  είναι ρητοί.]
είναι ρητοί.]Και η άσκηση στο πρωτότυπο: Μαυρογιάννης
Συντονιστής: nkatsipis
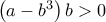 , τότε ο
, τότε ο 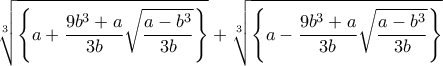
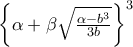 , όπου οι
, όπου οι  και
και  είναι ρητοί.]
είναι ρητοί.] είναι ρητοί.
είναι ρητοί. 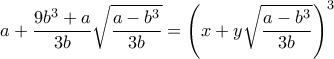 ,
,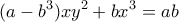 και
και 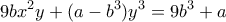
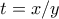 , κι αφού διαιρέσουμε τις παραπάνω με
, κι αφού διαιρέσουμε τις παραπάνω με  και μετά τις προκύπτουσες κατά μέλη παίρνουμε
και μετά τις προκύπτουσες κατά μέλη παίρνουμε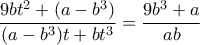
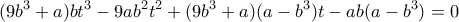
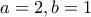 , παίρνουμε την
, παίρνουμε την 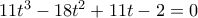
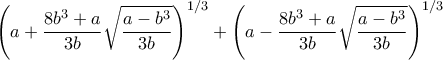
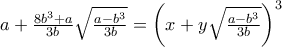
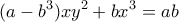 και
και 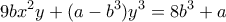
 και
και  .
.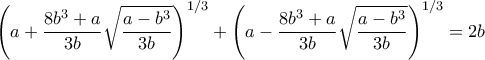 .
.Θα ήθελα να κάνω ένα σχόλιο για να γίνει κατανοητό αυτό που λέει ο Αχιλλέας.achilleas έγραψε:Με την παρούσα μορφή δεν κατάφερα να λύσω την άσκηση:
Καταρχήν φαντάζομαι ότι ο Hardy παραλείπει να αναφέρει ότι οιείναι ρητοί.
**************************************************************************************************
Πρώτα ας δούμε τι γίνεται με την πρωτότυπη άσκηση:
Αν θέσουμε,
μετά τις πράξεις παίρνουμε το σύστημα:
και
Θέτουμε, κι αφού διαιρέσουμε τις παραπάνω με
και μετά τις προκύπτουσες κατά μέλη παίρνουμε
η οποία μας δίνει
Θέτοντας, π.χ., παίρνουμε την
που δεν έχει ρητές ρίζες.
![\displaystyle {\sqrt[3]{a+\frac{9b^3+a}{3b}\sqrt{\frac{a-b^3}{3b}}} + \sqrt[3]{a-\frac{9b^3+a}{3b}\sqrt{\frac{a-b^3}{3b}}} = \left( x+y\sqrt{\frac{a-b^3}{3b}}\right) +\left( x-y\sqrt{\frac{a-b^3}{3b}\right)}=2x } \displaystyle {\sqrt[3]{a+\frac{9b^3+a}{3b}\sqrt{\frac{a-b^3}{3b}}} + \sqrt[3]{a-\frac{9b^3+a}{3b}\sqrt{\frac{a-b^3}{3b}}} = \left( x+y\sqrt{\frac{a-b^3}{3b}}\right) +\left( x-y\sqrt{\frac{a-b^3}{3b}\right)}=2x }](/forum/ext/geomar/texintegr/latexrender/pictures/4d861ca666955619a28ef6020909d71a.png)
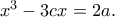
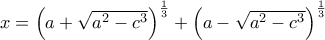 .
.![x=
\displaystyle {\sqrt[3]{a+\frac{8b^3+a}{3b}\sqrt{\frac{a-b^3}{3b}}} + \sqrt[3]{a-\frac{8b^3+a}{3b}\sqrt{\frac{a-b^3}{3b}}} x=
\displaystyle {\sqrt[3]{a+\frac{8b^3+a}{3b}\sqrt{\frac{a-b^3}{3b}}} + \sqrt[3]{a-\frac{8b^3+a}{3b}\sqrt{\frac{a-b^3}{3b}}}](/forum/ext/geomar/texintegr/latexrender/pictures/879c176c3145a8af0a9c9c5b16544b1f.png)
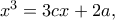 όπου
όπου ![c=\sqrt[3]{\big(a+\frac{8b^3+a}{3b}\sqrt{\frac{a-b^3}{3b}})\ctot\big(a-\frac{8b^3+a}{3b}\sqrt{\frac{a-b^3}{3b}}\big)}. c=\sqrt[3]{\big(a+\frac{8b^3+a}{3b}\sqrt{\frac{a-b^3}{3b}})\ctot\big(a-\frac{8b^3+a}{3b}\sqrt{\frac{a-b^3}{3b}}\big)}.](/forum/ext/geomar/texintegr/latexrender/pictures/214855352959059e3205baa2a26648ba.png)
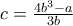 , ύστερα από πράξεις (εδώ ήταν το μυστικό των συγκεκριμένων ριζών!).
, ύστερα από πράξεις (εδώ ήταν το μυστικό των συγκεκριμένων ριζών!).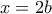 κ.τ.λ...
κ.τ.λ...Τελικά η άσκηση είναι λάθος.nsmavrogiannis έγραψε: 31. Αν, τότε ο
είναι ρητός
![\sqrt[3]{A} + \sqrt[3]{B} = p \sqrt[3]{A} + \sqrt[3]{B} = p](/forum/ext/geomar/texintegr/latexrender/pictures/db3a38f12978ee3912700802bc1d93e2.png) είναι ρητός, όπου Α, Β ακέραιοι, τότε υψώνοντας στον κύβο έχουμε
είναι ρητός, όπου Α, Β ακέραιοι, τότε υψώνοντας στον κύβο έχουμε ![A = (p - \sqrt[3]{B})^3 = p^3 - B - 3p \sqrt[3]{B}(p - \sqrt[3]{B}) = p^3 - B - 3p \sqrt[3]{B}\sqrt[3]{A} A = (p - \sqrt[3]{B})^3 = p^3 - B - 3p \sqrt[3]{B}(p - \sqrt[3]{B}) = p^3 - B - 3p \sqrt[3]{B}\sqrt[3]{A}](/forum/ext/geomar/texintegr/latexrender/pictures/233942c31c2e0c1783a3455c0e6be56d.png)
![\sqrt[3]{AB}= \frac{p^3-B-A}{3p} \sqrt[3]{AB}= \frac{p^3-B-A}{3p}](/forum/ext/geomar/texintegr/latexrender/pictures/391931f6e0284aa4a386b33e10d29579.png) = ρητός.
= ρητός.![\sqrt[3]{AB} \sqrt[3]{AB}](/forum/ext/geomar/texintegr/latexrender/pictures/8ea9232f3696d4fcdf2dec7cfd108ef5.png) .
.Πράγματι, ο τρόπος που έγραψα για το ζεύγοςMihalis_Lambrou έγραψε: Θα ήθελα να κάνω ένα σχόλιο για να γίνει κατανοητό αυτό που λέει ο Αχιλλέας.
Πολύ σωστά επισημαίνει ότι το a = 2, b=1 είναι αντιπαράδειγμα στην υπόδειξη του Hardy (που θέλει τα x, y και άρα το t = x/y ρητούς).
Προσοχή όμως, αυτό δεν σημαίνει ότι αναιρείται η αρχική άσκηση που ζητά να δείξουμε ότι είναι ρητός ο
Δηλαδή, δεν μας νοιάζει αν είναι ρητός ο y. Μόνο ο x μας ενδιαφέρει.
Δεν ξέρω την απάντηση, αλλά θα το ψάξω.
Φιλικά,
Μιχάλης Λάμπρου
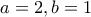 είναι αντιπαράδειγμα στην υπόδειξη του Hardy.
είναι αντιπαράδειγμα στην υπόδειξη του Hardy.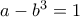 με
με  (οπότε
(οπότε  ) για να ισχύει η συνθήκη της υπόθεσης, και εξέτασα την παράσταση
) για να ισχύει η συνθήκη της υπόθεσης, και εξέτασα την παράσταση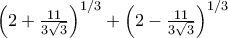 .
.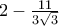 είναι αρνητικός οπότε θα πρέπει να είμαστε προσεκτικοί.
είναι αρνητικός οπότε θα πρέπει να είμαστε προσεκτικοί. και μετά από τη δυσκολία που συνάντησα, έθεσαachilleas έγραψε:
και
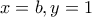 που μου φαινόταν ως "φυσιολογική" λύση.Τότε είδα ότι
που μου φαινόταν ως "φυσιολογική" λύση.Τότε είδα ότι 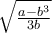 είναι άρρητος. Όμως η περίπτωση αυτή είναι αρκετή για να μαντέψουμε τη λύση
είναι άρρητος. Όμως η περίπτωση αυτή είναι αρκετή για να μαντέψουμε τη λύση 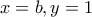 και να συνεχίσουμε.
και να συνεχίσουμε. πρέπει να είναι ρητός.
πρέπει να είναι ρητός. Σε αυτό το συμπέρασμα είχαμε καταλήξει και εμείς με τον Μανώλη αλλά είμαστε πολύ επιφυλακτικοί. Ο λόγος είναι ότι το συγκεκριμένο βιβλίο έκανε μία πανηγυρική, λόγω εκατονταετίας, ανατύπωση της 10ης έκδοσης με νέο πρόλογο γραμμένο από τον T. W. Körner. Στην έκδοση αυτή η άσκηση είναι ίδια και απαράλλαχτη. Σκεφτήκαμε πως με τόσες χιλιάδες, αν όχι εκατομμύρια μάτια που έχουν περάσει πάνω από το βιβλίο τα παροράματα θα έχουν πλέον αναιχνευθεί και διορθωθεί.Mihalis_Lambrou έγραψε: Τελικά η άσκηση είναι λάθος.
Μιχάλη η απόδειξη σου είναι πολύ κομψή (όλως δευτερεύον: εκεί που λες "όπου Α, Β ακέραιοι" νομίζω ότι ταιριάζει καλλίτερα το ρητοί). Η απόδειξη που έχουμε με τον Μανώλη είναι πολύ πιό εκτενής. Θα την ανεβάσω σύντομα χάριν βιοποικιλότητας.Mihalis_Lambrou έγραψε: Ανείναι ρητός, όπου Α, Β ακέραιοι, τότε υψώνοντας στον κύβο έχουμε
δηλαδή= ρητός.
Όμως εύκολα βρίσκουμε παραδείγματα (π.χ. α = 4, β = 1, άρα Α = 65, Β = -9) που δίνουν άρρητο
Ναι Νίκο, το έχω υπόψη. Έγραψα "ακέραιοι" για να φανεί το λάθος της άσκησης ακόμη και με περιορισμό των συνθηκών.nsmavrogiannis έγραψε:εκεί που λες "όπου Α, Β ακέραιοι" νομίζω ότι ταιριάζει καλλίτερα το ρητοί.
Ανεβάζω τις αποδείξεις που κάναμε για το εσφαλμένο της άσκησης το καλοκαίρι ο Μανώλης Ζαμπετάκης (ο οποίος ήταν και εκείνος που εντόπισε ότι η άσκηση είναι λάθος) και εγώ.nsmavrogiannis έγραψε: Η απόδειξη που έχουμε με τον Μανώλη είναι πολύ πιό εκτενής. Θα την ανεβάσω σύντομα χάριν βιοποικιλότητας.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες