george visvikis έγραψε: ↑Δευ Ιαν 06, 2025 1:36 pm
Η πλευρά

τριγώνου

είναι σταθερή κατά θέση και μέγεθος, ενώ η κορυφή

κινείται σε ευθεία
παράλληλη στη

και σε απόσταση

από αυτήν. Αν η

είναι διχοτόμος και η

διάμεσος του
τριγώνου, να βρείτε συναρτήσει του

τα ακρότατα του εμβαδού

καθώς και τις τιμές των

που αντιστοιχούν σε αυτά.
Μπορείτε να γενικεύσετε για

και

Τι παρατηρείτε;
Γιώργο και Θανάση καλημέρα...
Για το ανωτέρω ερώτημα παραθέτω και τα δικά μου ευρήματα:
Το εμβαδόν του τριγώνου

το θεώρησα από τη συνάρτηση:

όπου η μεταβλητή

είναι η τετμημένη του σημείου

Μελετὠντας τώρα τη συνάρτηση αυτή ψηφιακά (γιατί όχι;;) βρήκα τα ακόλουθα:
1η Περίπτωση:
Είναι:

Τότε προέκυψε το ακόλουθο σχήμα:

- Ακρότατα Εμβαδού 1.png (24.4 KiB) Προβλήθηκε 371 φορές
Στο σχήμα αυτό βλέπει κανείς το γράφημα της συνάρτησης

, το διάνυσμα

, τα ακρότατα
καθώς και τους δυο γεωμετρικούς τόπους που διατρέχουν τα δυο ακρότατα.
2η Περίπτωση
Το ύψος

είναι ανεξάρτητο της τιμής του

Τότε έχουμε το ακόλουθο σχήμα:

- Ακρότατα εμβαδού 2.png (28.66 KiB) Προβλήθηκε 371 φορές
Τα αντίστοιχα στοιχεία φαίνονται και στο σχήμα αυτό.
Οι γεωμετρικοί τόποι προκύπτουν μεταβάλλοντας αντίστοιχα τα μεγέθη

και

.
Η μεταβολή του

δίνει δυο παράλληλες ευθείες ενώ η μεταβολή του

δίνει δυο καμπύλες
που διαγράφουν αντίστοιχα τα δυο σημεία των ακροτάτων.
Παραθέτω και τις διευθύνσεις των δυναμικών αρχείων για καλύτερη εποπτεία!
1ο Σχήμα https://www.geogebra.org/m/cb2kqkvn
2ο Σχήμα https://www.geogebra.org/m/psjyyh8c
Κώστας Δόρτσιος
 τριγώνου
τριγώνου  είναι σταθερή κατά θέση και μέγεθος, ενώ η κορυφή
είναι σταθερή κατά θέση και μέγεθος, ενώ η κορυφή  κινείται σε ευθεία
κινείται σε ευθεία  και σε απόσταση
και σε απόσταση  από αυτήν. Αν η
από αυτήν. Αν η  είναι διχοτόμος και η
είναι διχοτόμος και η  διάμεσος του
διάμεσος του  τα ακρότατα του εμβαδού
τα ακρότατα του εμβαδού  καθώς και τις τιμές των
καθώς και τις τιμές των 
 και
και  Τι παρατηρείτε;
Τι παρατηρείτε;
 . Το ύψος του
. Το ύψος του  , είναι σταθερό
, είναι σταθερό  , άρα αναζητούμε
, άρα αναζητούμε  . Αλλά :
. Αλλά :  . Αν
. Αν  η προβολή του
η προβολή του 
 με μέγιστο :
με μέγιστο :  , για
, για  και
και 
 για :
για : 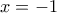 και :
και :  .
.
 ,
, το ελάχιστο και για
το ελάχιστο και για  το μέγιστο .
το μέγιστο . και μάλιστα συμμετρικά ...
και μάλιστα συμμετρικά ... το θεώρησα από τη συνάρτηση:
το θεώρησα από τη συνάρτηση:
 είναι η τετμημένη του σημείου
είναι η τετμημένη του σημείου 

 , το διάνυσμα
, το διάνυσμα  , τα ακρότατα
, τα ακρότατα  είναι ανεξάρτητο της τιμής του
είναι ανεξάρτητο της τιμής του 