Σελίδα 1 από 1
Ισότητα από άλλη ισότητα
Δημοσιεύτηκε: Σάβ Ιαν 04, 2025 8:19 pm
από KARKAR
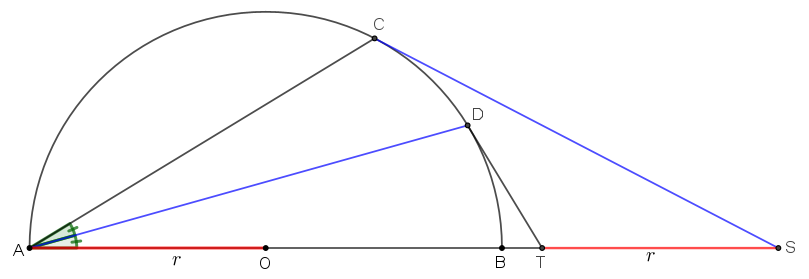
- Ισότητα από άλλη ισότητα.png (17.85 KiB) Προβλήθηκε 473 φορές
Το

είναι σημείο του ημικυκλίου διαμέτρου

και η

είναι η διχοτόμος της

.
Οι εφαπτόμενες του τόξου στα

τέμνουν την προέκταση της

στα σημεία

αντίστοιχα .
Αν :
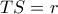
, εξετάστε αν είναι και :
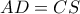
.
Re: Ισότητα από άλλη ισότητα
Δημοσιεύτηκε: Σάβ Ιαν 04, 2025 10:53 pm
από Mihalis_Lambrou
Αποσύρω την λύση ως εσφαλμένη, αλλά θα επανέλθω με σωστή.
Αποδεικνύεται ότι υπάρχει μία και μοναδική

ώστε να ισχύει η εν λόγω ισότητα.
Ζητώ συγγνώμη.

Re: Ισότητα από άλλη ισότητα
Δημοσιεύτηκε: Κυρ Ιαν 05, 2025 9:10 am
από Mihalis_Lambrou
Απέσυρα το προηγούμενο ως εσφαλμένο.
Συνεπώς η άσκηση είναι ακόμα ανοικτή.
Έχω σωστή λύση, παραλλαγή της εσφαλμένης, την οποία θα γράψω κάποια στιγμή.
Re: Ισότητα από άλλη ισότητα
Δημοσιεύτηκε: Κυρ Ιαν 05, 2025 10:28 am
από george visvikis
KARKAR έγραψε: ↑Σάβ Ιαν 04, 2025 8:19 pm
Ισότητα από άλλη ισότητα.pngΤο

είναι σημείο του ημικυκλίου διαμέτρου

και η

είναι η διχοτόμος της

.
Οι εφαπτόμενες του τόξου στα

τέμνουν την προέκταση της

στα σημεία

αντίστοιχα .
Αν :
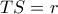
, εξετάστε αν είναι και :
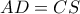
.
Θέτω
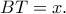
Είναι,
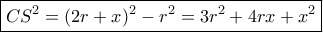

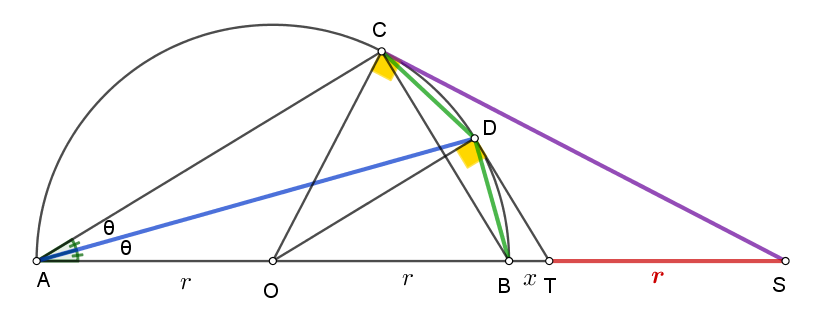
- Ισότητα από άλλη ισότητα.png (24.91 KiB) Προβλήθηκε 385 φορές
Εξάλλου με νόμο συνημιτόνου στο

έχω:
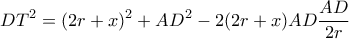
κι επειδή
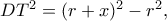
θα είναι
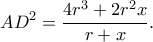
Αν τώρα είναι
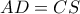
από την

καταλήγω στην εξίσωση
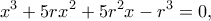
όπου με χρήση λογισμικού βρίσκω μοναδική λύση
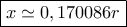
Re: Ισότητα από άλλη ισότητα
Δημοσιεύτηκε: Τετ Ιαν 08, 2025 10:26 am
από KARKAR
Κάνω μια ( ημιτελή )προσπάθεια :
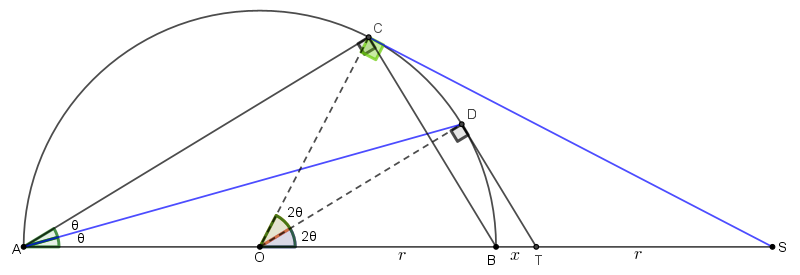
- is from is.png (24.32 KiB) Προβλήθηκε 340 φορές
Από το
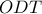
, είναι :
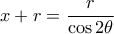
και από το
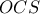
είναι :
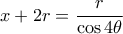
.
Λύνοντας ως προς

καταλήγουμε ότι για την γωνία

, ισχύει :
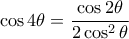
(*).
(Σημειώστε ότι η γωνία αυτή έχει μέτρο περίπου
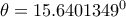
) . Καλούμαστε λοιπόν
να δείξουμε ότι αν ισχύει η (*) , τότε :
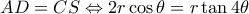
ή :
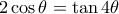
, η οποία ελέγχθηκε ( με λογισμικό) ότι ισχύει .
Κάποιος περισσότερο επίμονος ίσως πάρει την δόξα της "παλληκαρήσιας" απόδειξης

Re: Ισότητα από άλλη ισότητα
Δημοσιεύτηκε: Τετ Ιαν 08, 2025 11:32 am
από Mihalis_Lambrou
KARKAR έγραψε: ↑Τετ Ιαν 08, 2025 10:26 am
ή :
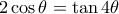
, η οποία ελέγχθηκε ( με λογισμικό) ότι ισχύει .
Κάποιος περισσότερο επίμονος ίσως πάρει την δόξα της "παλληκαρήσιας" απόδειξης

Θανάση, παραπάνω όταν έγραφα ότι έχω λύση της άσκησης την οποία θα αναρτήσω, αυτήν ακριβώς την ακριβή απόδειξη είχα κατά νου. Δηλαδή την ισοδυναμία (με χρήση Τριγωνομετρίας, όχι λογισμικού)
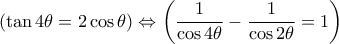
(η δεύτερη είναι άλλη μορφή της (*) που αναφέρεσαι).
Θα την αναρτήσω κάποια στιγμή. Με αποτρέπει προσωρινά ο φόρτος εργασίας και διάφορες ομιλίες που έχω στο εξωτερικό, με Zoom. Το χρωστάω. Υπομονή.)
Re: Ισότητα από άλλη ισότητα
Δημοσιεύτηκε: Τετ Ιαν 08, 2025 7:24 pm
από Mihalis_Lambrou
KARKAR έγραψε: ↑Σάβ Ιαν 04, 2025 8:19 pm
Το

είναι σημείο του ημικυκλίου διαμέτρου

και η

είναι η διχοτόμος της

.
Οι εφαπτόμενες του τόξου στα

τέμνουν την προέκταση της

στα σημεία

αντίστοιχα .
Αν :
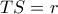
, εξετάστε αν είναι και :
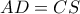
.
α) Έχουμε
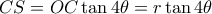
και
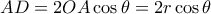
. Άρα η
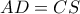
ισοδυναμεί με την
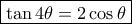
β) Από τα τρίγωνα
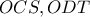
έχουμε
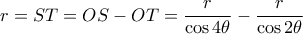
άρα
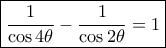
Θα δείξουμε τώρα την ισοδύναμία στα α), β) δείχνοντας ότι και τα δύο είναι ισοδύμαμα με την
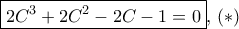
όπου
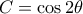
.
Σημειώνω ότι υπάρχει και καλύτερος τρόπος να δείξουμε την ισοδυναμία αλλά προτιμώ τον παρόντα γιατί τουλάχιστον μας επιτρέπει να βρούμε, μέσω λύσης της τριτοβάθμιας, την τιμή της γωνίας

που δίνει την ισότητα των τμημάτων.
Είναι α)
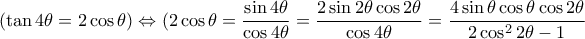
ισοδύναμα
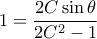
από όπου
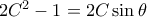
. Υψώνοντας στο τετράγωνο έχουμε
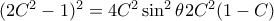
και άρα
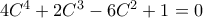
, ισοδύναμα
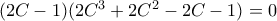
. Όμως
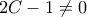
διότι δίνει

που απορρίπτεται γιατί το σχήμα απαιτεί
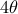
οξεία.
Τελικά ισχύει η

. Το βήμα αυτό αντιστρέφεται ακριβώς διότι
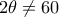
.
β) Είναι
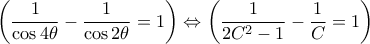
από όπου αμέσως η

, και η απόδειξη ολοκληρώθηκε.
 είναι σημείο του ημικυκλίου διαμέτρου
είναι σημείο του ημικυκλίου διαμέτρου  και η
και η  είναι η διχοτόμος της
είναι η διχοτόμος της  .
. τέμνουν την προέκταση της
τέμνουν την προέκταση της  στα σημεία
στα σημεία  αντίστοιχα .
αντίστοιχα .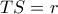 , εξετάστε αν είναι και :
, εξετάστε αν είναι και : 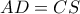 .
. είναι σημείο του ημικυκλίου διαμέτρου
είναι σημείο του ημικυκλίου διαμέτρου  και η
και η  είναι η διχοτόμος της
είναι η διχοτόμος της  .
. τέμνουν την προέκταση της
τέμνουν την προέκταση της  στα σημεία
στα σημεία  αντίστοιχα .
αντίστοιχα .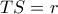 , εξετάστε αν είναι και :
, εξετάστε αν είναι και : 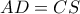 .
. ώστε να ισχύει η εν λόγω ισότητα.
ώστε να ισχύει η εν λόγω ισότητα.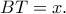 Είναι,
Είναι, 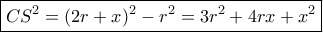

 έχω:
έχω: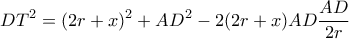 κι επειδή
κι επειδή 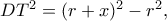
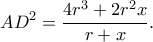 Αν τώρα είναι
Αν τώρα είναι 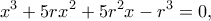 όπου με χρήση λογισμικού βρίσκω μοναδική λύση
όπου με χρήση λογισμικού βρίσκω μοναδική λύση 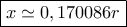
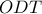 , είναι :
, είναι : 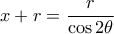 και από το
και από το 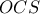 είναι :
είναι : 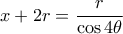 .
. καταλήγουμε ότι για την γωνία
καταλήγουμε ότι για την γωνία  , ισχύει :
, ισχύει : 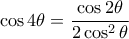 (*).
(*).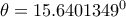 ) . Καλούμαστε λοιπόν
) . Καλούμαστε λοιπόν 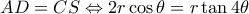
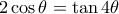 , η οποία ελέγχθηκε ( με λογισμικό) ότι ισχύει .
, η οποία ελέγχθηκε ( με λογισμικό) ότι ισχύει .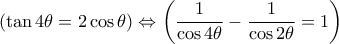
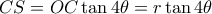 και
και 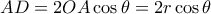 . Άρα η
. Άρα η 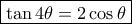
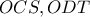 έχουμε
έχουμε 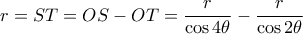 άρα
άρα 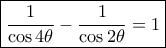
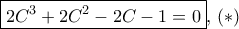 όπου
όπου 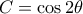 .
. 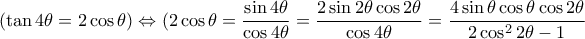 ισοδύναμα
ισοδύναμα 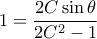 από όπου
από όπου 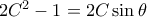 . Υψώνοντας στο τετράγωνο έχουμε
. Υψώνοντας στο τετράγωνο έχουμε 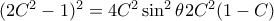 και άρα
και άρα 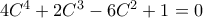 , ισοδύναμα
, ισοδύναμα 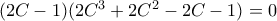 . Όμως
. Όμως 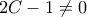 διότι δίνει
διότι δίνει  που απορρίπτεται γιατί το σχήμα απαιτεί
που απορρίπτεται γιατί το σχήμα απαιτεί 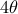 οξεία.
οξεία.  . Το βήμα αυτό αντιστρέφεται ακριβώς διότι
. Το βήμα αυτό αντιστρέφεται ακριβώς διότι 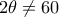 .
.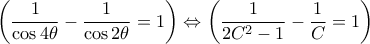 από όπου αμέσως η
από όπου αμέσως η