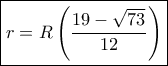να κατασκευάσει ένα βράχο τόσο βαρύ , που να μην μπορεί και ο ίδιος να τον σηκώσει !
Σε σημείο
 της διαμέτρου
της διαμέτρου  ενός ημικυκλίου , υψώνω το κάθετο τμήμα
ενός ημικυκλίου , υψώνω το κάθετο τμήμα 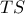 . Σχεδιάζω
. Σχεδιάζω στο ίδιο ημιεπίπεδο ημικύκλιο διαμέτρου
 προς το οποίο φέρω την εφαπτομένη
προς το οποίο φέρω την εφαπτομένη  .
.Βρείτε την θέση του
 , για την οποία μεγιστοποιείται το τμήμα
, για την οποία μεγιστοποιείται το τμήμα  . Χωρίς λύση !
. Χωρίς λύση !
 το μεγάλο και
το μεγάλο και  το μικρό ημικύκλιο. Προφανώς,
το μικρό ημικύκλιο. Προφανώς, 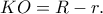
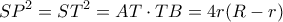
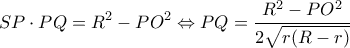

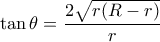 βρίσκω
βρίσκω 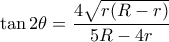 και στη συνέχεια
και στη συνέχεια 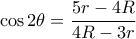
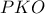 υπολογίζω το
υπολογίζω το  και αντικαθιστώ στην
και αντικαθιστώ στην 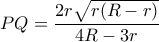
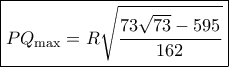 όταν
όταν