Δι-αγωνία
Συντονιστής: gbaloglou
Δι-αγωνία
Στο κυρτό τετράπλευρο του σχήματος , ας προσπαθήσουμε να απαντήσουμε στα εξής :
α) Όταν η μία διαγώνιος αυξάνει η άλλη μειώνεται ;
β) Πότε οι δύο διαγώνιοι θα γίνουν ίσες ;
γ) Πότε θα μεγιστοποιηθεί το άθροισμα των δύο διαγωνίων ;
α) Όταν η μία διαγώνιος αυξάνει η άλλη μειώνεται ;
β) Πότε οι δύο διαγώνιοι θα γίνουν ίσες ;
γ) Πότε θα μεγιστοποιηθεί το άθροισμα των δύο διαγωνίων ;
Λέξεις Κλειδιά:
-
Ιάσων Κωνσταντόπουλος
- Δημοσιεύσεις: 30
- Εγγραφή: Κυρ Ιαν 28, 2024 10:16 pm
- Επικοινωνία:
Re: Δι-αγωνία (CAS assisted)
Θεωρούμε ένα ορθοκανονικό σύστημα συντεταγμένων ώστε
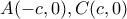 με
με  .
. Από την τριγωνική ανισότητα θα έχουμε
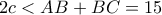 .
. Το
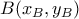 θα είναι σημείο τομής των κύκλων
θα είναι σημείο τομής των κύκλων 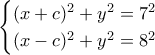
Επειδή
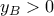 βρίσκουμε
βρίσκουμε 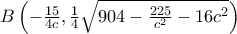 .
.Το
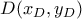 θα είναι σημείο τομής των κύκλων
θα είναι σημείο τομής των κύκλων 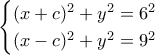
Επειδή
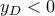 βρίσκουμε
βρίσκουμε 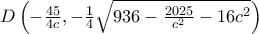 .
.Επειδή το
 είναι κυρτό, οι διαγώνιοι
είναι κυρτό, οι διαγώνιοι  θα τέμνονται σε εσωτερικό τους σημείο. Από αυτό βρίσκουμε
θα τέμνονται σε εσωτερικό τους σημείο. Από αυτό βρίσκουμε 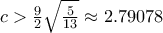 .
. Για
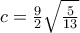 τα σημεία
τα σημεία  είναι συνευθειακά ενώ για
είναι συνευθειακά ενώ για 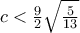 το τετράπλευρο δεν είναι κυρτό.
το τετράπλευρο δεν είναι κυρτό.Στη συνέχεια ορίζουμε
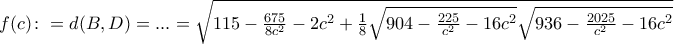 ,
,  όπου
όπου 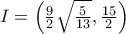 .
.Σε αυτό το σημείο μπορούμε να μεταφράσουμε τα ερωτήματα του προβλήματος σε ερωτήματα για την
 .
.Ερώτημα #1: Είναι η
 γνησίως φθίνουσα;
γνησίως φθίνουσα;Ερώτημα #2: Να μελετηθεί η εξίσωση
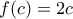
Ερώτημα #3: Να βρεθεί το ολικό μέγιστο της συνάρτησης
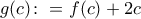
Απάντηση στο #1
Με επίπονες, αλλά απλές πράξεις, βρίσκουμε ότι η εξίσωση
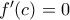 δεν έχει λύση στο διάστημα
δεν έχει λύση στο διάστημα  αν και αξίζει να σημειωθεί ότι
αν και αξίζει να σημειωθεί ότι 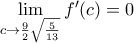 .
. η
η 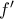 διατηρεί πρόσημο στο
διατηρεί πρόσημο στο  (θεώρημα Darboux)
(θεώρημα Darboux)  η
η  είναι γνησίως μονότονη και μάλιστα φθίνουσα αφού
είναι γνησίως μονότονη και μάλιστα φθίνουσα αφού 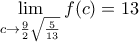 και
και 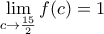
Απάντηση στο #2
Η ισότητα
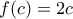 συνεπάγεται
συνεπάγεται 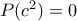 όπου
όπου 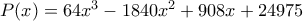 . Υπάρχει μοναδική επιτρεπτή τιμή για το
. Υπάρχει μοναδική επιτρεπτή τιμή για το  για την οποία έχουμε
για την οποία έχουμε 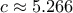 . Η τιμή αυτή μπορεί να εκφραστεί σε κλειστή μορφή:
. Η τιμή αυτή μπορεί να εκφραστεί σε κλειστή μορφή: 
Απάντηση στο #3
Η
 παρουσιάζει ολικό μέγιστο στο εσωτερικό του διαστήματος
παρουσιάζει ολικό μέγιστο στο εσωτερικό του διαστήματος  . Πιο συγκεκριμένα με απλές αλλά επίπονες πράξεις μπορούμε να δείξουμε ότι η ισότητα
. Πιο συγκεκριμένα με απλές αλλά επίπονες πράξεις μπορούμε να δείξουμε ότι η ισότητα 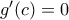 συνεπάγεται ότι το
συνεπάγεται ότι το  είναι ρίζα της εξίσωσης
είναι ρίζα της εξίσωσης  όπου
όπου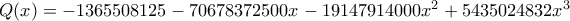
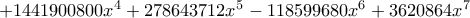
Υπάρχει μοναδική αποδεκτή τιμή για το
 , την οποία θα συμβολίσουμε με
, την οποία θα συμβολίσουμε με  , για την οποία έχουμε
, για την οποία έχουμε 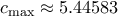

Σημείωση: Μερικές γεωμετρικές συνθήκες που οδηγούν σε τιμές για το
 που έχουν κάποια εγγύτητα με την τιμή
που έχουν κάποια εγγύτητα με την τιμή  είναι οι εξής:
είναι οι εξής:i)
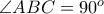 για
για 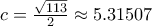
ii)
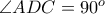 για
για 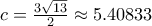
iii)
 εγγράψιμο για
εγγράψιμο για 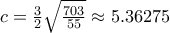
Η προαναφερθείσα εγγύτητα ήταν τέτοια ώστε ατενίζοντας το σχήμα κατά την ανάλυση του προβλήματος, υπήρξε έστω και βραχυπρόθεσμα η ελπίδα/υποψία ότι το
 λαμβάνεται όταν ισχύει μια από αυτές τις συνθήκες, αλλά φευ...
λαμβάνεται όταν ισχύει μια από αυτές τις συνθήκες, αλλά φευ...Ιάσων Κωνσταντόπουλος
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες
