 χωρίσαμε την σταθερού μήκους υποτείνουσα
χωρίσαμε την σταθερού μήκους υποτείνουσα  , ενός - μεταβλητών κάθετων πλευρών -
, ενός - μεταβλητών κάθετων πλευρών -ορθογωνίου τριγώνου
 , σε τμήματα :
, σε τμήματα : 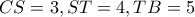 . Πως πρέπει να σχεδιαστεί
. Πως πρέπει να σχεδιαστεί το τρίγωνο αυτό , ώστε :
 ; Εικασία : στην θέση αυτή , έχουμε μεγιστοποίηση της γωνίας
; Εικασία : στην θέση αυτή , έχουμε μεγιστοποίηση της γωνίας  .
.
 είναι
είναι  τότε αφού
τότε αφού 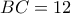 , έπεται ότι οι συνταταγμένες του
, έπεται ότι οι συνταταγμένες του 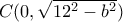 . Επίσης από το Θεώρημα του Θαλή έπεται ότι είναι
. Επίσης από το Θεώρημα του Θαλή έπεται ότι είναι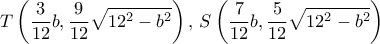
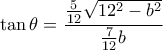 και
και 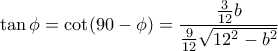
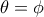 δίνει
δίνει 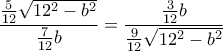 .
.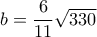 .
. επιτυγχάνεται όταν
επιτυγχάνεται όταν 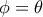
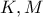 οι προβολές των
οι προβολές των 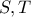 στις πλευρές
στις πλευρές 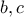 του τριγώνου
του τριγώνου  .
. 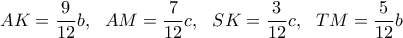
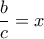
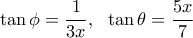 οπότε
οπότε 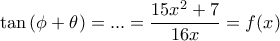
 έχει ελάχιστο όταν
έχει ελάχιστο όταν 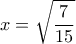
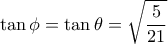
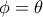 και, με τη βοήθεια του πυθαγορείου θεωρήματος....
και, με τη βοήθεια του πυθαγορείου θεωρήματος....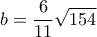 .
.
