Μόνο ίσοι κύκλοι

∫ot.T. · #1

Έστω τρίγωνο ABC και D σημείο που κινείται στην ευθεία της διχοτόμου της γωνίας Α. Η κάθετη ευθεία στην διχοτόμο που διέρχεται από το D τέμνει τις AB, AC στα P, Q αντίστοιχα.Έστω Η το σημείο του φορέα της PQ με την ιδιότητα οι περιγεγραμμένοι κύκλοι των BPH και CQH να είναι ίσοι. Έστω R το δεύτερο σημείο τομής τους, αν έχουν, αλλιώς το R ταυτίζεται με το Η. Από το R φέρουμε παράλληλη στην PQ, που θα τέμνει τις AB, AC στα S, T αντίστοιχα. Από τα S, T φέρουμε κάθετες στον φορέα του BC που θα τον τέμνει στα N, M αντίστοιχα. Να αποδειχθεί ότι αν και μόνο αν το ABC είναι ισοσκελές τότε οι περιγεγραμμένοι κύκλοι των NBA, MCA θα είναι ίσοι.

∫ot.T. · #2

Επαναφορά!

∫ot.T. · #3

Καλά Χριστούγεννα!

Επειδή δεν έχει αναρτηθεί κάποια λύση θα μου επιτρέψετε να δημοσιεύσω την δική μου.

Αφού η AD είναι διχοτόμος της 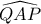$\widehat{QAP}$ και κάθετη στην BC τότε AQ=AP

Οπότε θα ισχύει πως 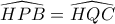$\widehat{HPB} = \widehat{HQC}$ άρα HB=HC

αφού από υπόθεση οι κύκλοι 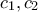$c_{1}, c_{2}$ του σχήματος είναι ίσοι.

Άρα το Η είναι σημείο της μεσοκαθέτου τόσο των δύο κέντρων των κύκλων όσο και της BC, άρα οι δύο μεσοκάθετοι
ταυτίζονται, κάτι που οδηγεί στο γεγονός ότι RB=RC

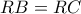,όντας το R σημείο της μεσοκαθέτου των δύο κέντρων.

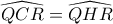Έχουμε $\widehat{PBR}=\widehat{PHR}$ και $\widehat{QCR}=\widehat{QHR}$ από εγγράψιμα τετράπλευρα
Άρα $\widehat{PBR}+\widehat{QCR}=180^{\circ}\Leftrightarrow \widehat{ABR}+\widehat{ACR}=180^{\circ}$
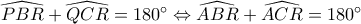
Άρα τα A, B, C, R είναι ομοκυκλικά.
Αφού όμως το R διχοτομεί την BC τότε διχοτομεί και το ομώνυμο τόξο, άρα τα D, A, R συνευθυακά.

Από υπόθεση και από την τελευταία πρόταση έχουμε $ST \perp AR\Leftrightarrow SR=TR$
Αν ονομάσουμε το μέσο της BC Κ, τότε RK είναι διάμεσος του τραπεζιού STMN επειδή
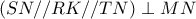$(SN//RK//TN)\perp MN$ και SR=ST

Οπότε $NK = MK\Leftrightarrow BN=CM$

Αν το ABC είναι ισοσκελές τότε $\widehat{ABC}=\widehat{ACM}, AB=AC, NB=MC$
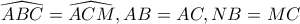
Άρα τα τρίγωνα ΑΝΒ, ΑMC, είναι ίσα, το ίδιο και οι περιγεγραμμένοι κύκλοι τους.

Αν οι κύκλοι των ABN, ACM είναι ίσοι τότε 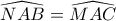$\widehat{NAB}=\widehat{MAC}$ , αφού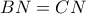 BN=CN

Οπότε τα N, M πρέπει να ισαπέχουν από το σημείο K και $\widehat{NAR}=\widehat{MAR}$
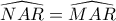
Όμως ήδη τα B,C ισαπέχουν από το Κ και ισχύει πως $\widehat{BAR}=\widehat{CAR}$

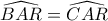
Δεν υπάρχουν, όμως, άλλα σημεία με αυτές τις ιδιότητες που έχουν τα B, C εκτός αν AB = AC
Επειδή τα Ν, Μ τις έχουν αυτές τις ιδιότητες, πρέπει το τρίγωνο ABC να είναι ισοσκελές.

Η αλήθεια της πρότασης με κόκκινα γράμματα έχει αποδειχθεί με διάφορους τρόπους στην ανάρτηση μου:«Υπάρχουν άλλα;»

Θα ήθελα να δω και διαφορετικές προσεγγίσεις στο θέμα.

Μόνο ίσοι κύκλοι

Μόνο ίσοι κύκλοι

Re: Μόνο ίσοι κύκλοι

Re: Μόνο ίσοι κύκλοι

Μέλη σε σύνδεση