Για το θέμα που ακολουθεί έχω λύση , αλλά και την ..
Θεωρούμε τον ρόμβο
 . Οι
. Οι  τέμνονται στο
τέμνονται στο  , όπου
, όπου  και
και 
Να εξεταστεί αν ισχύει:
 . Σας ευχαριστώ εκ των προτέρων, Γιώργος.
. Σας ευχαριστώ εκ των προτέρων, Γιώργος.Συντονιστής: gbaloglou
 . Οι
. Οι  τέμνονται στο
τέμνονται στο  , όπου
, όπου  και
και 
 . Σας ευχαριστώ εκ των προτέρων, Γιώργος.
. Σας ευχαριστώ εκ των προτέρων, Γιώργος.ΈστωΓιώργος Μήτσιος έγραψε: ↑Τετ Οκτ 18, 2023 11:58 pmΧαιρετώ.
Για το θέμα που ακολουθεί έχω λύση , αλλά και την .... προσδοκία για κομψότερη λύση απ' αυτή που βρήκα..
Θεωρούμε τον ρόμβο. Οι
τέμνονται στο
, όπου
και
18-10 Ίσοι λόγοι σε ρόμβο.png
Να εξεταστεί αν ισχύει:. Σας ευχαριστώ εκ των προτέρων, Γιώργος.
 . Τότε τα τρίγωνα
. Τότε τα τρίγωνα  είναι ισεμβαδικά αντίστοιχα με τα
είναι ισεμβαδικά αντίστοιχα με τα  (μια κοινή πλευρά και οι τρίτες κορυφές τους σε ευθεία παράλληλη στην κοινή πλευρά) , τα οποία τρίγωνα έχουν ίσα ύψη
(μια κοινή πλευρά και οι τρίτες κορυφές τους σε ευθεία παράλληλη στην κοινή πλευρά) , τα οποία τρίγωνα έχουν ίσα ύψη  (ύψη ρόμβου) ως προς τις πλευρές τους
(ύψη ρόμβου) ως προς τις πλευρές τους  .
.
 με κοινό ύψος από την κοινή τους κορυφή
με κοινό ύψος από την κοινή τους κορυφή  θα είναι
θα είναι  και ομοίως
και ομοίως 
 και με δεδομένο ότι
και με δεδομένο ότι  (αφού
(αφού  παραλληλόγραμμο) προκύπτει ότι :
παραλληλόγραμμο) προκύπτει ότι : 
 και
και 
 κατά μέλη και δεδομένου ότι
κατά μέλη και δεδομένου ότι  προκύπτει ότι:
προκύπτει ότι: 
 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.ΕίναιΓιώργος Μήτσιος έγραψε: ↑Τετ Οκτ 18, 2023 11:58 pmΧαιρετώ.
Για το θέμα που ακολουθεί έχω λύση , αλλά και την .... προσδοκία για κομψότερη λύση απ' αυτή που βρήκα..
Θεωρούμε τον ρόμβο. Οι
τέμνονται στο
, όπου
και
18-10 Ίσοι λόγοι σε ρόμβο.png
Να εξεταστεί αν ισχύει:. Σας ευχαριστώ εκ των προτέρων, Γιώργος.
 και
και  επομένως θα αποδείξουμε ότι
επομένως θα αποδείξουμε ότι 
 με διατέμνουσα
με διατέμνουσα  δίνει
δίνει 
 συνεπώς θα δείξουμε ότι
συνεπώς θα δείξουμε ότι 
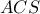 με διατέμνουσα
με διατέμνουσα  δίνει
δίνει  και το ζητούμενο αποδείχτηκε
και το ζητούμενο αποδείχτηκεΜέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες