 , να βρεθεί ο αριθμός των ριζών
, να βρεθεί ο αριθμός των ριζών της εξίσωσης :
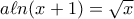 .
.Συντονιστής: emouroukos
 , να βρεθεί ο αριθμός των ριζών
, να βρεθεί ο αριθμός των ριζών 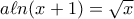 .
.• Αν
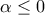 , μοναδική ρίζα είναι η
, μοναδική ρίζα είναι η 
 και
και  , είναι ισοδύναμη με την
, είναι ισοδύναμη με την 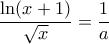 (1)
(1)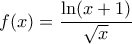 ,
,
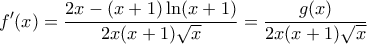 , όπου
, όπου 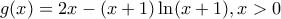
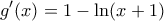 και
και 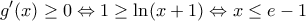
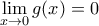 και
και 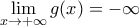
 έχει ολικό μέγιστο για
έχει ολικό μέγιστο για  το
το 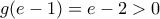
 της
της  (άρα και της
(άρα και της  ) με
) με 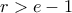 .
. είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο ![\displaystyle (0,r] \displaystyle (0,r]](/forum/ext/geomar/texintegr/latexrender/pictures/b450ca0352c01c5c827d62cc29da1f31.png) και γνησίως φθίνουσα στο
και γνησίως φθίνουσα στο 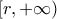 .
. 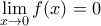 ,
,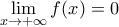 (εύκολα με κανόνες De l Hospital)
(εύκολα με κανόνες De l Hospital)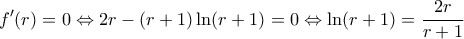
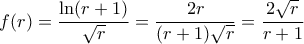
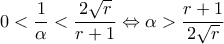 , η (1) έχει δύο ρίζες (και την
, η (1) έχει δύο ρίζες (και την  )
)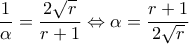 , η (1) έχει μία ρίζα , την
, η (1) έχει μία ρίζα , την  (και την
(και την  )
)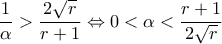 η (1) έχει ρίζα μόνο την
η (1) έχει ρίζα μόνο την 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες