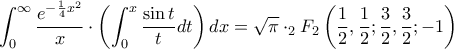 , όπου με το σύμβολο
, όπου με το σύμβολο 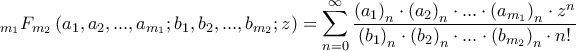 ορίζεται η υπεργεωμετρική συνάρτηση και
ορίζεται η υπεργεωμετρική συνάρτηση και 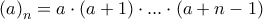 είναι το σύμβολο του Pochammer.
είναι το σύμβολο του Pochammer.Υ.Γ Επειδή μπορεί να αποδειχθεί δύσκολη, θα αφήσω όσο χρόνο χρειαστεί μέχρι να βάλω τη λύση μου.
Συντονιστής: emouroukos
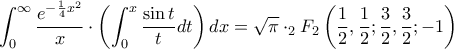 , όπου με το σύμβολο
, όπου με το σύμβολο 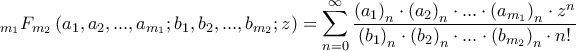 ορίζεται η υπεργεωμετρική συνάρτηση και
ορίζεται η υπεργεωμετρική συνάρτηση και 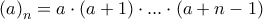 είναι το σύμβολο του Pochammer.
είναι το σύμβολο του Pochammer.Θα γράψω λύση κάποια στιγμή (όχι τώρα γιατί η πληκτολόγιση είναι επίπονη). Για την ώρα έχω διάφορα σχόλια.
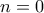 . Επειδή τυχαίνει να το γνωρίζω, είναι
. Επειδή τυχαίνει να το γνωρίζω, είναι 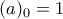 .
. 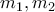 , όταν το μόνο που θέλει η άσκηση είναι το
, όταν το μόνο που θέλει η άσκηση είναι το 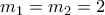 . Στα Μαθηματικά πρέπει να κρατάμε τα πράγματα στην απαιτούμενη απλότητα, χωρίς να συσκοτίζουμε την εικόνα με συμβολισμούς που δίνουν την εντύπωση ότι η άσκηση είναι πολύπλοκη ενώ στην πραγματικότητα είναι σχετικά απλή. Πόσο μάλλον όταν στην συγκεκριμένη άσκηση όπου έχουμε
. Στα Μαθηματικά πρέπει να κρατάμε τα πράγματα στην απαιτούμενη απλότητα, χωρίς να συσκοτίζουμε την εικόνα με συμβολισμούς που δίνουν την εντύπωση ότι η άσκηση είναι πολύπλοκη ενώ στην πραγματικότητα είναι σχετικά απλή. Πόσο μάλλον όταν στην συγκεκριμένη άσκηση όπου έχουμε  και
και  . Εδώ ο γενικός όρος της σειράς είναι απλά
. Εδώ ο γενικός όρος της σειράς είναι απλά 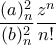 (και ακριβέστερα, με
(και ακριβέστερα, με 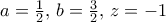 )
) είναι μόλις μία μονάδα παραπάνω από τα
είναι μόλις μία μονάδα παραπάνω από τα  , δηλαδή
, δηλαδή  , υπάρχει μία μεγάλη απλοποίηση στην υπεργεωμετρική σειρά. Εν ολίγοις, μετά τις άμεσες απλοποιήσεις, η σειρά έχει γενικό όρο απλά τον
, υπάρχει μία μεγάλη απλοποίηση στην υπεργεωμετρική σειρά. Εν ολίγοις, μετά τις άμεσες απλοποιήσεις, η σειρά έχει γενικό όρο απλά τον 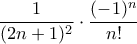 δηλαδή το ζητούμενο είναι να δείξουμε ότι
δηλαδή το ζητούμενο είναι να δείξουμε ότι 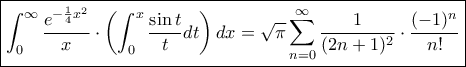
 μέσα στο ολοκλήρωμα και μετά ολοκληρώνουμε όρο προς όρο. Θα χρειαστούν τα ολοκληρώματα
μέσα στο ολοκλήρωμα και μετά ολοκληρώνουμε όρο προς όρο. Θα χρειαστούν τα ολοκληρώματα 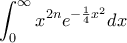 , που είναι γνωστά: συνήθως δίνονται συναρτήσει του
, που είναι γνωστά: συνήθως δίνονται συναρτήσει του 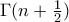 , αλλά μπορούμε και ευκολότερα.
, αλλά μπορούμε και ευκολότερα. μέσα στο άθροισμα να πρέπει να γίνει
μέσα στο άθροισμα να πρέπει να γίνει 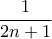 (χωρίς τετράγωνο). Θα το ελέγξω, αλλά για την ώρα ας μας πει ο θεματοθέτης αν έχω δίκιο.
(χωρίς τετράγωνο). Θα το ελέγξω, αλλά για την ώρα ας μας πει ο θεματοθέτης αν έχω δίκιο.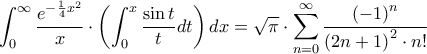 που προκύπτει από την διαδικασία που λέτε. Αναπτύσσω το
που προκύπτει από την διαδικασία που λέτε. Αναπτύσσω το  σε δυναμοσειρά (προφανώς μέσα στο ολοκλήρωμα) και ... μετά χρησιμοποιώ τον μετασχηματισμό του Laplace και τη συνάρτηση
σε δυναμοσειρά (προφανώς μέσα στο ολοκλήρωμα) και ... μετά χρησιμοποιώ τον μετασχηματισμό του Laplace και τη συνάρτηση  . Βέβαια, η δική σας λύση υποθέτω είναι πιο σύντομη, εγώ έχω μια λίγο μπελαλίδικη απόδειξη. Όσον αφορά τα σχόλια:
. Βέβαια, η δική σας λύση υποθέτω είναι πιο σύντομη, εγώ έχω μια λίγο μπελαλίδικη απόδειξη. Όσον αφορά τα σχόλια: 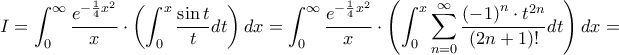
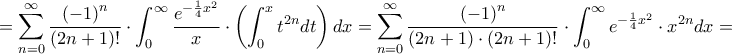
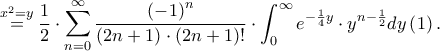
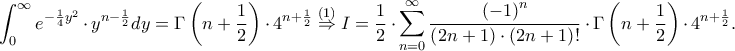
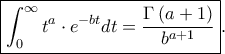
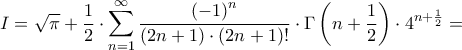
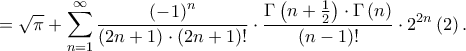
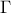 ισχύει
ισχύει 
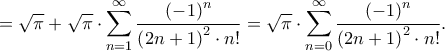
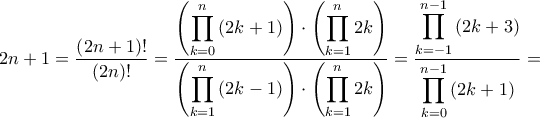
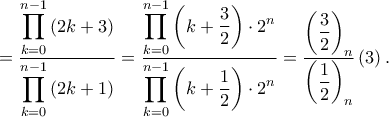
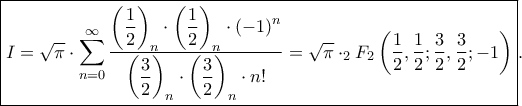
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες