![f : [0,1] \rightarrow \mathbb{R} f : [0,1] \rightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/a18fddcc23773f998a47d61c24e21010.png) μια συνεχής συνάρτηση και
μια συνεχής συνάρτηση και  ένας θετικός αριθμός. Να δείξετε ότι υπάρχει
ένας θετικός αριθμός. Να δείξετε ότι υπάρχει  τέτοιο, ώστε
τέτοιο, ώστε
για κάθε
![x,y \in [0,1] x,y \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/8ccc5717da3dd0b073cc7bf160912733.png) .
.Συντονιστής: emouroukos
![f : [0,1] \rightarrow \mathbb{R} f : [0,1] \rightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/a18fddcc23773f998a47d61c24e21010.png) μια συνεχής συνάρτηση και
μια συνεχής συνάρτηση και  ένας θετικός αριθμός. Να δείξετε ότι υπάρχει
ένας θετικός αριθμός. Να δείξετε ότι υπάρχει  τέτοιο, ώστε
τέτοιο, ώστε
![x,y \in [0,1] x,y \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/8ccc5717da3dd0b073cc7bf160912733.png) .
. είναι συνεχής σε κλειστό διάστημα, τότε είναι ομοιόμορφα συνεχής σε αυτό. Άρα για κάθε
είναι συνεχής σε κλειστό διάστημα, τότε είναι ομοιόμορφα συνεχής σε αυτό. Άρα για κάθε  υπάρχει
υπάρχει  ώστε
ώστε 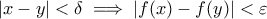 για κάθε
για κάθε ![x,y \in [0,1] x,y \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/8ccc5717da3dd0b073cc7bf160912733.png) . Επίσης είναι και φραγμένη σε αυτό, έστω
. Επίσης είναι και φραγμένη σε αυτό, έστω 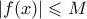 για κάθε
για κάθε ![x \in [0,1] x \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/c75c22c0876976bad2957525698cc870.png) .
.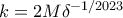 . Για
. Για ![x,y \in [0,1] x,y \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/8ccc5717da3dd0b073cc7bf160912733.png) :
: , τότε
, τότε 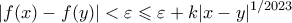
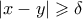 , τότε
, τότε 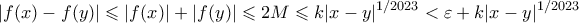
Αλλιώς (ουσιαστικά είναι παραλλαγή, αλλά για να υπάρχει): Από ομοιόμορφη συνέχεια, για το δεδομένοΟρέστης Λιγνός έγραψε: ↑Πέμ Αύγ 17, 2023 9:28 amΈστωμια συνεχής συνάρτηση και
ένας θετικός αριθμός. Να δείξετε ότι υπάρχει
τέτοιο, ώστε
για κάθε.
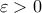 υπάρχει
υπάρχει  τέτοιο ώστε
τέτοιο ώστε 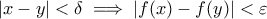 για κάθε
για κάθε ![x,y \in [0,1] x,y \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/de37f4027d82ef7aca71540ac8b41e38.png) .
.  το αποδεικτέο είναι άμεσο αφού τότε
το αποδεικτέο είναι άμεσο αφού τότε 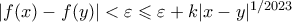 .
. ![x,y \in [0,1] x,y \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/8ccc5717da3dd0b073cc7bf160912733.png) με
με 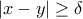 . To σύνολο αυτό, δηλαδή το
. To σύνολο αυτό, δηλαδή το ![\{(x,y) \in \mathbb [0,1]\times [0,1]: |x-y| \ge \delta \} \{(x,y) \in \mathbb [0,1]\times [0,1]: |x-y| \ge \delta \}](/forum/ext/geomar/texintegr/latexrender/pictures/7ae989a35db47eeae3be8df3dcac12e2.png) είναι κλειστό (διότι αν
είναι κλειστό (διότι αν 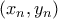 ακολουθία του που συγκλίνει στο
ακολουθία του που συγκλίνει στο  είναι άμεσο ότι και το
είναι άμεσο ότι και το  βρίσκεται στο σύνολο). Είναι και φραγμένο, άρα συμπαγές. Έπεται ότι, σε αυτό το σύνολο, η συνάρτηση
βρίσκεται στο σύνολο). Είναι και φραγμένο, άρα συμπαγές. Έπεται ότι, σε αυτό το σύνολο, η συνάρτηση 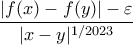
 τέτοιο ώστε
τέτοιο ώστε 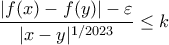 , που ισοδυναμεί με την ζητούμενη.
, που ισοδυναμεί με την ζητούμενη.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες