
Ποιό είναι το εμβαδόν του;
Συντονιστής: nsmavrogiannis

nsmavrogiannis έγραψε: ↑Κυρ Απρ 30, 2023 12:10 pmΟι πλευρές ενός τριγώνου είναι ρίζες της εξίσωσης
Ποιό είναι το εμβαδόν του;
 είναι η ημιπερίμετρος ,
είναι η ημιπερίμετρος ,  η ακτίνα του εγγεγραμμένου κύκλου και
η ακτίνα του εγγεγραμμένου κύκλου και  του παραγεγραμμένου κύκλου τότε οι ρίζες της εξίσωσης
του παραγεγραμμένου κύκλου τότε οι ρίζες της εξίσωσης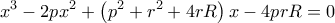
 . Είναι ακόμη
. Είναι ακόμη 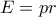 και
και  .
. 
Έστωnsmavrogiannis έγραψε: ↑Κυρ Απρ 30, 2023 12:10 pmΟι πλευρές ενός τριγώνου είναι ρίζες της εξίσωσης
Ποιό είναι το εμβαδόν του;
 οι πλευρές του τριγώνου και
οι πλευρές του τριγώνου και  το εμβαδόν του. Με τον τύπο του Ήρωνα
το εμβαδόν του. Με τον τύπο του Ήρωνα 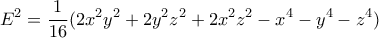

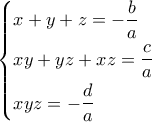

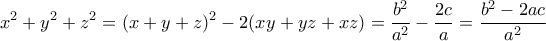

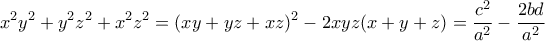

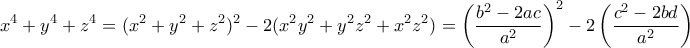
 παίρνουμε μετά τις πράξεις
παίρνουμε μετά τις πράξεις 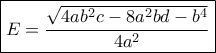
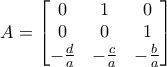 (companion matrix).
(companion matrix). , ισχύει:
, ισχύει: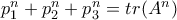
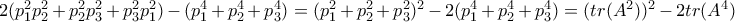 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες