Αστειεύομαι
 Μέρος 1: Οι ευθείς
Μέρος 1: Οι ευθείς 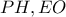 τέμνονται πάνω στον κύκλο
τέμνονται πάνω στον κύκλο  .
. Έστω η αρνητική αντιστροφή
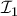
με πόλο

και ακτίνα
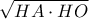
. Αυτή η αντιστροφή στέλνει το σημείο

στο

, το

στο

και τούμπαλιν. Επιλέον, αν η ημιευθεία
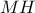
τέμνει τον κύκλο

στο σημείο

, τότε τα σημεία
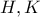
είναι αντίστροφα, καθώς
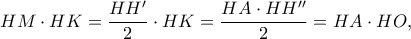
όπου
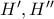
τα σημεία τομής των ημιευθειών
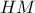
και

με τον κύκλο

.
Συνεπώς, ο κύκλος

έχει ως εικόνα την ευθεία
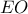
, και ο κύκλος
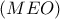
τον κύκλο
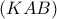
, δηλαδή τον κύκλο

. Άρα, αν η ευθεία
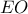
τέμνει τον

στα σημεία

, με το

προς το μέρος του

ως προς την

, τότε τα σημεία
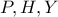
και
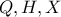
είναι συνευθειακά, καθώς τα σημεία

είναι οι εικόνες των σημείων
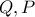
αντίστοιχα στην αντιστροφή
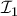
.
Μέρος 2: Οι ευθείς 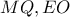 τέμνονται πάνω στον κύκλο
τέμνονται πάνω στον κύκλο  .
. Έστω η αντιστροφή
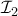
με πόλο

και ακτίνα

. Αυτή η αντιστροφή κρατά σταθερά τα σημεία
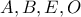
, και στέλνει το σημείο

στο σημείο

, καθώς
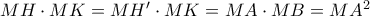
.
Συνεπώς, η εικόνα του κύκλου

είναι ο κύκλος

, και η εικόνα του κύκλου
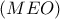
η ευθεία
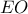
. Άρα, οι εικόνες των σημείων

είναι τα σημεία

, αντίστοιχα, πράγμα που σημαίνει ότι τα σημεία
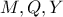
είναι συνευθειακά, δηλαδή η ευθεία

περνά από το σημείο

, όπως θέλαμε.
Συνδυάζοντας τα δύο αποτελέσματα, έχουμε το ζητούμενο.
 σημείο του άξονα
σημείο του άξονα 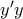 με
με 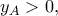
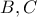 σημεία του άξονα
σημεία του άξονα 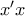 τέτοια ώστε
τέτοια ώστε 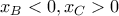 και το τρίγωνο
και το τρίγωνο  είναι οξυγώνιο. Έστω
είναι οξυγώνιο. Έστω  ύψος,
ύψος,  ορθόκεντρο και
ορθόκεντρο και  μέσο της πλευράς
μέσο της πλευράς  του τριγώνου
του τριγώνου  και
και  η αρχή των αξόνων. Οι περιγεγραμμένοι κύκλοι των τριγώνων
η αρχή των αξόνων. Οι περιγεγραμμένοι κύκλοι των τριγώνων 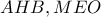 τέμνονται στα σημεία
τέμνονται στα σημεία  με το
με το  προς το μέρος του
προς το μέρος του  ως προς
ως προς 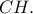 Ερώτημα: Να εξετάσετε αν οι ευθείες
Ερώτημα: Να εξετάσετε αν οι ευθείες 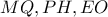 συντρέχουν (και μάλιστα σε σημείο του κύκλου
συντρέχουν (και μάλιστα σε σημείο του κύκλου  ).
).
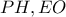 τέμνονται πάνω στον κύκλο
τέμνονται πάνω στον κύκλο  . Έστω η αρνητική αντιστροφή
. Έστω η αρνητική αντιστροφή 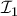 με πόλο
με πόλο 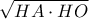 . Αυτή η αντιστροφή στέλνει το σημείο
. Αυτή η αντιστροφή στέλνει το σημείο  στο
στο  και τούμπαλιν. Επιλέον, αν η ημιευθεία
και τούμπαλιν. Επιλέον, αν η ημιευθεία 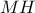 τέμνει τον κύκλο
τέμνει τον κύκλο  , τότε τα σημεία
, τότε τα σημεία 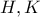 είναι αντίστροφα, καθώς
είναι αντίστροφα, καθώς 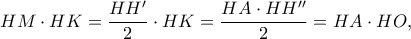
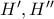 τα σημεία τομής των ημιευθειών
τα σημεία τομής των ημιευθειών 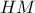 και
και  με τον κύκλο
με τον κύκλο  έχει ως εικόνα την ευθεία
έχει ως εικόνα την ευθεία 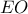 , και ο κύκλος
, και ο κύκλος 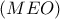 τον κύκλο
τον κύκλο 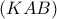 , δηλαδή τον κύκλο
, δηλαδή τον κύκλο  , με το
, με το  προς το μέρος του
προς το μέρος του  , τότε τα σημεία
, τότε τα σημεία 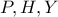 και
και 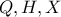 είναι συνευθειακά, καθώς τα σημεία
είναι συνευθειακά, καθώς τα σημεία 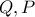 αντίστοιχα στην αντιστροφή
αντίστοιχα στην αντιστροφή 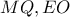 τέμνονται πάνω στον κύκλο
τέμνονται πάνω στον κύκλο 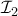 με πόλο
με πόλο  . Αυτή η αντιστροφή κρατά σταθερά τα σημεία
. Αυτή η αντιστροφή κρατά σταθερά τα σημεία 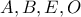 , και στέλνει το σημείο
, και στέλνει το σημείο 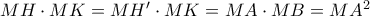 .
. είναι συνευθειακά, δηλαδή η ευθεία
είναι συνευθειακά, δηλαδή η ευθεία  περνά από το σημείο
περνά από το σημείο  , όπως θέλαμε.
, όπως θέλαμε.