Για
 να αποδειχθεί ότι οι
να αποδειχθεί ότι οι  και
και  είναι αντίστροφοι αν και μόνο αν οι
είναι αντίστροφοι αν και μόνο αν οι  και
και  είναι αντίθετοι.
είναι αντίθετοι.Συντονιστής: nsmavrogiannis
 να αποδειχθεί ότι οι
να αποδειχθεί ότι οι  και
και  είναι αντίστροφοι αν και μόνο αν οι
είναι αντίστροφοι αν και μόνο αν οι  και
και  είναι αντίθετοι.
είναι αντίθετοι.Το αντίστροφο είναι εύκολο.nsmavrogiannis έγραψε: ↑Δευ Μαρ 06, 2023 12:42 amΓιανα αποδειχθεί ότι οι
και
είναι αντίστροφοι αν και μόνο αν οι
και
είναι αντίθετοι.
 , η οποία είναι θετική, γνησίως αύξουσα και
, η οποία είναι θετική, γνησίως αύξουσα και 


 και πολλαπλασιάζοντας κατά μέλη τις
και πολλαπλασιάζοντας κατά μέλη τις  έχουμε:
έχουμε:![\displaystyle{ 4=(x+y)^2-\left(\frac{1}{x}-\frac{1}{y}\right)^2\Leftrightarrow .... (xy-1)\left[(x+y)^2(xy+1)-4xy\right]=0 \ \ \bf(3)} \displaystyle{ 4=(x+y)^2-\left(\frac{1}{x}-\frac{1}{y}\right)^2\Leftrightarrow .... (xy-1)\left[(x+y)^2(xy+1)-4xy\right]=0 \ \ \bf(3)}](/forum/ext/geomar/texintegr/latexrender/pictures/0458c95f295ea12d7e3f3cbbcfd36ae1.png)
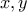 θετικοί θα είναι:
θετικοί θα είναι:  και έτσι από την
και έτσι από την  έχουμε
έχουμε  .
.



 και την υπερβολική εφαπτόμενη
και την υπερβολική εφαπτόμενη 
 ,
,  ,
,  ,
, 
 ,
,  ,
, 
 ,
,  , για κάθε
, για κάθε 
 έχει σύνολο τιμών το
έχει σύνολο τιμών το  . Θέτουμε
. Θέτουμε  και
και 








![2\sinh\left(\frac{x+y}{2}\right)\left[\sinh\left(\frac{x+y}{2}\right)+\cosh\left(\frac{x+y}{2}\right)\cosh(x-y)\right]=0 \overset{(\star)}{\Rightarrow} 2\sinh\left(\frac{x+y}{2}\right)\left[\sinh\left(\frac{x+y}{2}\right)+\cosh\left(\frac{x+y}{2}\right)\cosh(x-y)\right]=0 \overset{(\star)}{\Rightarrow}](/forum/ext/geomar/texintegr/latexrender/pictures/b6378c8ca4ea6939365bcaf10da7f96e.png)
 .
. 
 Είναι
Είναι 
 , αδύνατο.
, αδύνατο. και
και  η
η  είναι το υπερβολικό ημίτονο.
είναι το υπερβολικό ημίτονο.  θά έχουμε το σύστημα:
θά έχουμε το σύστημα:
 βρίσκουμε
βρίσκουμε
 όπου
όπου 
 διαιρεί το
διαιρεί το  και επομένως ή θα είναι
και επομένως ή θα είναι  είτε
είτε  όπου
όπου  είναι το πηλίκο της διαίρεσης δηλαδή το
είναι το πηλίκο της διαίρεσης δηλαδή το  . Είναι
. Είναι  επομένως
επομένως  και
και  . Αντικαθιστώντας στην
. Αντικαθιστώντας στην 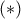 βρίσκουμε τελικά ότι
βρίσκουμε τελικά ότι  (αδύνατη) ή
(αδύνατη) ή  . Η τελευταία δίνει και
. Η τελευταία δίνει και  . Από αυτές με εύκολη πορεία μέσω περιπτώσεων καταλήγουμε στο αποδεικτέο.
. Από αυτές με εύκολη πορεία μέσω περιπτώσεων καταλήγουμε στο αποδεικτέο.Αν ηnsmavrogiannis έγραψε: ↑Δευ Μαρ 13, 2023 1:22 amΓεια σας
Σας ευχαριστώ για τις απαντήσεις σας. Ενδιαφέρον είναι ότι υπερβολικές συναρτήσεις που πρωταγωνιστούν στην λύση του Στράτη υπάρχουν αφανείς και στην πρώτη λύση του συναδέλφου abgd αφού μεκαι
η
είναι το υπερβολικό ημίτονο.
Η δική μου "brute force" λύση υπολείπεται σε συντομία και κομψότητα και την αναφέρω συνοπτικά:
Αν ονομάσουμεθά έχουμε το σύστημα:
Λύνοντας την πρώτη εξίσωση του συστήματος ως προςβρίσκουμε
και αντικαθιστώντας στην δεύτερη βρίσκουμε τελικάόπου
Εϋκολα βρίσκουμε ότι τοδιαιρεί το
και επομένως ή θα είναι
είτε
όπου
είναι το πηλίκο της διαίρεσης δηλαδή το
. Είναι
επομένως
και
. Αντικαθιστώντας στην
βρίσκουμε τελικά ότι
(αδύνατη) ή
. Η τελευταία δίνει και
. Από αυτές με εύκολη πορεία μέσω περιπτώσεων καταλήγουμε στο αποδεικτέο.



Σταύρο πράγματι το θέμα μπορεί να εξεταστεί σε γενικότερο πλαίσιο. Από την στιγμή που υποτεθεί ότι δουλεύουμε σε ένα σώμαΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τρί Μαρ 14, 2023 1:35 pm
Αν η
γραφεί

τότε η απόδειξη δίνει το ζητούμενο σε κάθε σώμα.(Θα πρέπει επιπλέον να υποθέσουμε ότι οι ρίζες ανήκουν στο σώμα)
Είναι λοιπόν πολύ γενικότερη από τις δύο παραπάνω αποδείξεις οι οποίες χρησιμοποιούν
σαν σώμα το
 και για τα στ
και για τα στ έχουμε σε μία επάκταση του
έχουμε σε μία επάκταση του  τις ρίζες των
τις ρίζες των  ,
,  όλη η εργασία μπορεί να διεκπεραιωθεί στο
όλη η εργασία μπορεί να διεκπεραιωθεί στο  . Οι παραγοντοποιήσεις των πολυωνύμων είναι ρητές στο
. Οι παραγοντοποιήσεις των πολυωνύμων είναι ρητές στο  και δεν χρησιμοποιείται καθόλου η διάταξη. Είναι χαρακτηριστικό ότι όταν ζητήσουμε από το Maple να λύσει το σύστημα
και δεν χρησιμοποιείται καθόλου η διάταξη. Είναι χαρακτηριστικό ότι όταν ζητήσουμε από το Maple να λύσει το σύστημα  δίνοντας:
δίνοντας: είναι αντίθετες ρίζες του
είναι αντίθετες ρίζες του  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης