Δίνονται οι διακεκριμένοι αριθμοί αριθμοί
 ,
,  , ...,
, ...,  και οι αριθμοί
και οι αριθμοί  ,
,  ,...,
,...,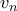 . Ένα πολυώνυμο
. Ένα πολυώνυμο  διαιρούμενο με τα
διαιρούμενο με τα  ,
, 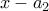 , ...,
, ..., 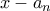 αφήνει υπόλοιπα
αφήνει υπόλοιπα  ,
,  ,...,
,...,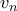 . Να βρεθεί το υπόλοιπο της διαίρεσης του
. Να βρεθεί το υπόλοιπο της διαίρεσης του  δια του
δια του 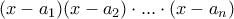 .
.Συντονιστής: nsmavrogiannis
 ,
,  , ...,
, ...,  και οι αριθμοί
και οι αριθμοί  ,
,  ,...,
,...,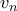 . Ένα πολυώνυμο
. Ένα πολυώνυμο  διαιρούμενο με τα
διαιρούμενο με τα  ,
, 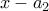 , ...,
, ..., 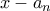 αφήνει υπόλοιπα
αφήνει υπόλοιπα  ,
,  ,...,
,...,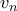 . Να βρεθεί το υπόλοιπο της διαίρεσης του
. Να βρεθεί το υπόλοιπο της διαίρεσης του  δια του
δια του 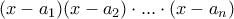 .
.Ενδιαφέρον. Δεν θυμάμαι να το έχω ξαναδεί.nsmavrogiannis έγραψε: ↑Σάβ Απρ 30, 2022 9:53 pmΓνωστό αλλά νομίζω ότι έχει ενδιαφέρον για συζήτηση στην τάξη. Δεν θυμάμαι αν το έχουμε συζητήσει.
Δίνονται οι διακεκριμένοι αριθμοί αριθμοί,
, ...,
και οι αριθμοί
,
,...,
. Ένα πολυώνυμο
διαιρούμενο με τα
,
, ...,
αφήνει υπόλοιπα
,
,...,
. Να βρεθεί το υπόλοιπο της διαίρεσης του
δια του
.
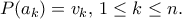
 δια του
δια του 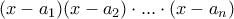 δίνει σχέση της μορφής
δίνει σχέση της μορφής 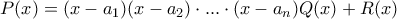 όπου το
όπου το  είναι ένα και μοναδικό πολυώνυμο βαθμού το πολύ
είναι ένα και μοναδικό πολυώνυμο βαθμού το πολύ  .
. 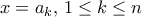 παίρνουμε
παίρνουμε 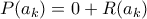 , δηλαδή
, δηλαδή 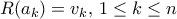 .
. μπορούμε να το βρούμε ως πολυώνυμο παρεμβολής Lagrange. Είναι το άθροισμα των πολυωνύμων
μπορούμε να το βρούμε ως πολυώνυμο παρεμβολής Lagrange. Είναι το άθροισμα των πολυωνύμων 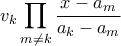 για
για 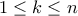 .
.Γεια σαςMihalis_Lambrou έγραψε: ↑Σάβ Απρ 30, 2022 10:16 pmΕνδιαφέρον. Δεν θυμάμαι να το έχω ξαναδεί.nsmavrogiannis έγραψε: ↑Σάβ Απρ 30, 2022 9:53 pmΓνωστό αλλά νομίζω ότι έχει ενδιαφέρον για συζήτηση στην τάξη. Δεν θυμάμαι αν το έχουμε συζητήσει.
Δίνονται οι διακεκριμένοι αριθμοί αριθμοί,
, ...,
και οι αριθμοί
,
,...,
. Ένα πολυώνυμο
διαιρούμενο με τα
,
, ...,
αφήνει υπόλοιπα
,
,...,
. Να βρεθεί το υπόλοιπο της διαίρεσης του
δια του
.
Από την υπόθεση έχουμε (απλό και γνωστό)
Η διαίρεση τουδια του
δίνει σχέση της μορφής
όπου το
είναι ένα και μοναδικό πολυώνυμο βαθμού το πολύ
.
Θέτονταςπαίρνουμε
, δηλαδή
.
Οπότε τομπορούμε να το βρούμε ως πολυώνυμο παρεμβολής Lagrange. Είναι το άθροισμα των πολυωνύμων
για
.
 είναι θεωρία του σχολικού. Για
είναι θεωρία του σχολικού. Για  είναι βασική άσκηση που την έχουν πολλά βιβλία. Για
είναι βασική άσκηση που την έχουν πολλά βιβλία. Για  τα πράγματα δυσκολεύουν διότι το σύστημα που οδηγεί στην εύρεση του πολυωνύμου
τα πράγματα δυσκολεύουν διότι το σύστημα που οδηγεί στην εύρεση του πολυωνύμου  έχει τις δυσκολίες του. Αν οι μαθητές έχουν θεωρία οριζουσών στην διάθεση τους (πιθανόν με τα νέα προγράμματα να έχουν) η ενασχόληση στην τάξη με αυτό το σύστημα έχει ενδιαφέρον αφού η ορίζουσα του είναι η Vandermonde.
έχει τις δυσκολίες του. Αν οι μαθητές έχουν θεωρία οριζουσών στην διάθεση τους (πιθανόν με τα νέα προγράμματα να έχουν) η ενασχόληση στην τάξη με αυτό το σύστημα έχει ενδιαφέρον αφού η ορίζουσα του είναι η Vandermonde. σημεία πράγμα ιδιαίτερα χρήσιμο αν διδάσκουμε προσεγγίσεις κάτι που φαντάζομαι ότι θα υπάρχει στα νέα προγράμματα. Εκτός από τα σχετικά λογισμικά έχουμε στην διάθεση μας και πολλούς υπολογιστές στο διαδίκτυο (ενδεικτικά https://www.dcode.fr/lagrange-interpolating-polynomial )
σημεία πράγμα ιδιαίτερα χρήσιμο αν διδάσκουμε προσεγγίσεις κάτι που φαντάζομαι ότι θα υπάρχει στα νέα προγράμματα. Εκτός από τα σχετικά λογισμικά έχουμε στην διάθεση μας και πολλούς υπολογιστές στο διαδίκτυο (ενδεικτικά https://www.dcode.fr/lagrange-interpolating-polynomial )Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες