 , είναι σώμα.
, είναι σώμα.Ερώτηση: Αν οι αριθμοί
 και
και  είναι αλγεβρικοί αριθμοί επί του σώματος
είναι αλγεβρικοί αριθμοί επί του σώματος 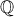 και έστω
και έστω ![\varphi_ {a} (x) \in \mathbb{Q}[x] \varphi_ {a} (x) \in \mathbb{Q}[x]](/forum/ext/geomar/texintegr/latexrender/pictures/52f0908e548b283b925345b5e6bce0dc.png) και
και ![\varphi_ {b}(x) \in \mathbb{Q}[x] \varphi_ {b}(x) \in \mathbb{Q}[x]](/forum/ext/geomar/texintegr/latexrender/pictures/d7245f2cbd5611cba94b49ad37f9dae8.png) τα ελαχιστικά πολυώνυμα των
τα ελαχιστικά πολυώνυμα των  και
και  , αντίστοιχα. Το ερώτημά μου είναι ποιο είναι το ελαχιστικό πολυώνυμο των αριθμών
, αντίστοιχα. Το ερώτημά μου είναι ποιο είναι το ελαχιστικό πολυώνυμο των αριθμών  και
και 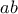 ;
; Μπορείτε να βοηθήσετε ως προς την επίλυση ή να μου πείτε που να ψάξω για να βρω την λύση.
Έχω την πεποίθηση ότι αν
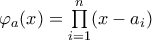 και
και 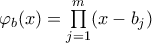 με τα
με τα 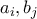 πιθανόν να μην ανήκουν όλοι στο
πιθανόν να μην ανήκουν όλοι στο  , ότι
, ότι 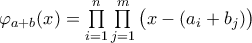 και
και 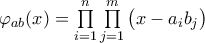 , απλά δεν γνωρίζω αν τα πολυώνυμα
, απλά δεν γνωρίζω αν τα πολυώνυμα 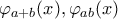 έχουν συντελεστές στο
έχουν συντελεστές στο  ;
;Για παράδειγμα, έστω ότι ο αριθμός
 είναι αλγεβρικός αριθμός επί του σώματος
είναι αλγεβρικός αριθμός επί του σώματος  βαθμού
βαθμού  και ας είναι
και ας είναι ![\varphi_{r}(x) = x^{n} + a_{n-1} x^{n-1} + a_{n-2} x^{n-2} + \cdots + a_{2} x^{2} + a_{1} x + a_{o} \in \mathbb{Q}[x] \varphi_{r}(x) = x^{n} + a_{n-1} x^{n-1} + a_{n-2} x^{n-2} + \cdots + a_{2} x^{2} + a_{1} x + a_{o} \in \mathbb{Q}[x]](/forum/ext/geomar/texintegr/latexrender/pictures/945d5c498e78c76b339b834cbbcf9ab9.png) , με
, με 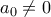 , το ελαχιστικό πολυώνυμο του
, το ελαχιστικό πολυώνυμο του  .
.Τότε ο
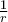 είναι αλγεβρικός αριθμός επί του σώματος
είναι αλγεβρικός αριθμός επί του σώματος  βαθμού
βαθμού  με ελαχιστικό πολυώνυμο
με ελαχιστικό πολυώνυμο ![\varphi_{\frac{1}{r}}(x) = x^{n} + \frac{a_{1}}{a_{0}} x^{n-1} + \frac{a_{2}}{a_{0}} x^{n-2} + \cdots + \frac{a_{n-2}}{a_{0}} x^{2} + \frac{a_{n-1}}{a_{0}} x + \frac{1}{a_{0}} \in \mathbb{Q}[x] \varphi_{\frac{1}{r}}(x) = x^{n} + \frac{a_{1}}{a_{0}} x^{n-1} + \frac{a_{2}}{a_{0}} x^{n-2} + \cdots + \frac{a_{n-2}}{a_{0}} x^{2} + \frac{a_{n-1}}{a_{0}} x + \frac{1}{a_{0}} \in \mathbb{Q}[x]](/forum/ext/geomar/texintegr/latexrender/pictures/b943e2d48133ff1c8d1b9618c8286121.png) , διότι
, διότι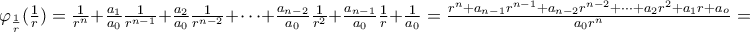
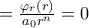 .
.Ελαχιστικό πολυώνυμο του αλγεβρικού αριθμού
 επί του σώματος
επί του σώματος  βαθμού
βαθμού  , το συμβολίζουμε
, το συμβολίζουμε ![\varphi_{c}(x) \in \mathbb{Q}[x] \varphi_{c}(x) \in \mathbb{Q}[x]](/forum/ext/geomar/texintegr/latexrender/pictures/063dc49686ddc80f3c961f249d5d59ae.png) χαρακτηρίζουμε το πολυώνυμο το οποίο είναι μη μηδενικό, έχει συντελεστές στους ρητούς αριθμούς, μονικό (ο μεγιστοβάθμιος συντελεστής ισούται με ένα), έχει ως ρίζα τον αριθμό
χαρακτηρίζουμε το πολυώνυμο το οποίο είναι μη μηδενικό, έχει συντελεστές στους ρητούς αριθμούς, μονικό (ο μεγιστοβάθμιος συντελεστής ισούται με ένα), έχει ως ρίζα τον αριθμό  και είναι αυτό με τον ελάχιστο βαθμό (δηλαδή δεν υπάρχει πολυώνυμο με τις παραπάνω ιδιότητες βαθμού μικρότερου ή ίσου του
και είναι αυτό με τον ελάχιστο βαθμό (δηλαδή δεν υπάρχει πολυώνυμο με τις παραπάνω ιδιότητες βαθμού μικρότερου ή ίσου του  ).
).
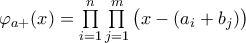 και
και 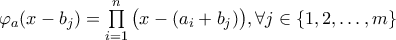 , οπότε
, οπότε ![\mathbb{Q}[x] \ni \prod\limits_{j=1}^{m} \varphi_{a}(x - b_{j}) = \prod\limits_{j=1}^{m} \prod\limits_{i=1}^{n} \big( x - ( a_{i} + b_{j} ) \big) = \varphi_{a+b}(x) \mathbb{Q}[x] \ni \prod\limits_{j=1}^{m} \varphi_{a}(x - b_{j}) = \prod\limits_{j=1}^{m} \prod\limits_{i=1}^{n} \big( x - ( a_{i} + b_{j} ) \big) = \varphi_{a+b}(x)](/forum/ext/geomar/texintegr/latexrender/pictures/b9b625a87744627ec18e92871d46c6c4.png) .
.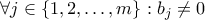 έχουμε
έχουμε 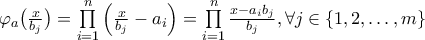 , οπότε
, οπότε ![\mathbb{Q}[x] \ni \prod\limits_{j=1}^{m} \varphi_{a} \big( \frac{x}{b_{j}} \big) = \frac{1}{\underbrace{b_{1} b_{2} \cdots b_{m}}_{\in \mathbb{Q}}} \prod\limits_{j=1}^{m} \prod\limits_{i=1}^{n} \big( x - a_{i} b_{j} ) \big) \mathbb{Q}[x] \ni \prod\limits_{j=1}^{m} \varphi_{a} \big( \frac{x}{b_{j}} \big) = \frac{1}{\underbrace{b_{1} b_{2} \cdots b_{m}}_{\in \mathbb{Q}}} \prod\limits_{j=1}^{m} \prod\limits_{i=1}^{n} \big( x - a_{i} b_{j} ) \big)](/forum/ext/geomar/texintegr/latexrender/pictures/a14cdde781e7fdd6b71b466e87dd5e1c.png) , άρα
, άρα 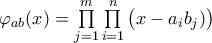 .
.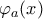 και
και 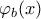 .
.