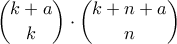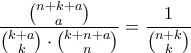και έστω
και έστω  ένας αυθαίρετος μη αρνητικός ακέραιος.
ένας αυθαίρετος μη αρνητικός ακέραιος. Επιλέγουμε τυχαία και ομοιόμορφα ένα υποσύνολο
 του
του 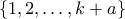 μεγέθους
μεγέθους  . (Δηλαδή όλα τα υποσύνολα μεγέθους
. (Δηλαδή όλα τα υποσύνολα μεγέθους  επιλέγονται με την ίδια πιθανότητα.)
επιλέγονται με την ίδια πιθανότητα.)Ανεξάρτητα του
 επιλέγουμε τυχαία και ομοιόμορφα ένα υποσύνολο
επιλέγουμε τυχαία και ομοιόμορφα ένα υποσύνολο  του
του 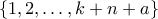 μεγέθους
μεγέθους  .
. Να δειχθεί ότι η πιθανότητα
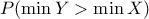
είναι ανεξάρτητη του


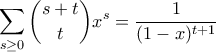
 φορές την γεωμετρική και λίγη απλή άλγεβρα. Διαλέγοντας πρώτα το μέγιστο στοιχείο του
φορές την γεωμετρική και λίγη απλή άλγεβρα. Διαλέγοντας πρώτα το μέγιστο στοιχείο του ![\displaystyle{\displaystyle{ \sum_{i=0}^{a } \binom{k-1 +i }{k -1 } \binom{ n + a - i }{ n } = \sum_{i=0}^{a} [x^{i}] (\frac{1}{(1-x)^{k}}) [x^{a-i}] (\frac{1}{(1-x)^{n+1}}) = [x^{a}] (\frac{1}{(1-x)^{n+k+1}}) = \binom{n+k+a}{a} } } \displaystyle{\displaystyle{ \sum_{i=0}^{a } \binom{k-1 +i }{k -1 } \binom{ n + a - i }{ n } = \sum_{i=0}^{a} [x^{i}] (\frac{1}{(1-x)^{k}}) [x^{a-i}] (\frac{1}{(1-x)^{n+1}}) = [x^{a}] (\frac{1}{(1-x)^{n+k+1}}) = \binom{n+k+a}{a} } }](/forum/ext/geomar/texintegr/latexrender/pictures/132a1568e82e095d8fd30d4316059e02.png)