 με πραγματικούς συντελεστές, όπου
με πραγματικούς συντελεστές, όπου  . Υποθέτουμε ότι το πολυώνυμο
. Υποθέτουμε ότι το πολυώνυμο  διαιρεί το
διαιρεί το  για κάποιο θετικό ακέραιο
για κάποιο θετικό ακέραιο  . Να αποδείξετε ότι:
. Να αποδείξετε ότι:
Συντονιστής: Demetres
 με πραγματικούς συντελεστές, όπου
με πραγματικούς συντελεστές, όπου  . Υποθέτουμε ότι το πολυώνυμο
. Υποθέτουμε ότι το πολυώνυμο  διαιρεί το
διαιρεί το  για κάποιο θετικό ακέραιο
για κάποιο θετικό ακέραιο  . Να αποδείξετε ότι:
. Να αποδείξετε ότι:
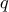 βαθμού το πολύ
βαθμού το πολύ  ισχύει η σχέση
ισχύει η σχέση 

 ).
). για το πολυώνυμο
για το πολυώνυμο 
 είναι το
είναι το  -στό πολυώνυμο Chebyshev, με:
-στό πολυώνυμο Chebyshev, με: , αν
, αν ![\displaystyle{x \in \left[ { - 1,1} \right]} \displaystyle{x \in \left[ { - 1,1} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/690ed97edebc27b407d2af36defb8457.png)
 αν
αν  .
. είναι
είναι 
 ,
,



 , για κάθε
, για κάθε 
 είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  και το ότι
και το ότι  για κάθε
για κάθε  ,
,
 .
. ,
,  και
και  , έχουμε ότι:
, έχουμε ότι:
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες