Θέματα της δεύτερης μέρας για την 9η τάξη.
1. Μια συνοικία αποτελείται από ένα τετράγωνο
 . Την νύχτα της πρωτοχρονιάς ξαφνικά χιόνισε και έκτοτε κάθε νύχτα σε κάθε κελί έπεφτε από
. Την νύχτα της πρωτοχρονιάς ξαφνικά χιόνισε και έκτοτε κάθε νύχτα σε κάθε κελί έπεφτε από  εκατοστά χιόνι, χιόνιζε μόνο τις νύχτες. Κάθε πρωί ένας οδοκαθαριστής καθαρίζει μια σειρά (γραμμή ή στήλη) και στοιβάζει από εκεί όλο το χιόνι σε μια από τις γειτονικές σειρές (σε κάθε κελί στο γειτονικό κατά πλευρά). Για παράδειγμα, μπορεί να διαλέξει την έβδομη στήλη και από κάθε κελί της να φτυαρίσει όλο το χιόνι στο αριστερά γειτονικό. Να στοιβάσει το χιόνι εκτός των ορίων της συνοικίας δεν επιτρέπεται. Την νύχτα της εκατοστής μέρας ο προϊστάμενος του γραφείου καθαριότητας επισκέπτεται την συνοικία και βρίσκει το κελί, που έχει την στοίβα χιονιού με το μεγαλύτερο ύψος. Ο σκοπός του οδοκαθαριστή είναι να επιτύχει, ώστε αυτό το ύψος να είναι το λιγότερο δυνατό. Τι ύψος στοίβας θα βρει ο προϊστάμενος; (Α. Σολύνιν )
εκατοστά χιόνι, χιόνιζε μόνο τις νύχτες. Κάθε πρωί ένας οδοκαθαριστής καθαρίζει μια σειρά (γραμμή ή στήλη) και στοιβάζει από εκεί όλο το χιόνι σε μια από τις γειτονικές σειρές (σε κάθε κελί στο γειτονικό κατά πλευρά). Για παράδειγμα, μπορεί να διαλέξει την έβδομη στήλη και από κάθε κελί της να φτυαρίσει όλο το χιόνι στο αριστερά γειτονικό. Να στοιβάσει το χιόνι εκτός των ορίων της συνοικίας δεν επιτρέπεται. Την νύχτα της εκατοστής μέρας ο προϊστάμενος του γραφείου καθαριότητας επισκέπτεται την συνοικία και βρίσκει το κελί, που έχει την στοίβα χιονιού με το μεγαλύτερο ύψος. Ο σκοπός του οδοκαθαριστή είναι να επιτύχει, ώστε αυτό το ύψος να είναι το λιγότερο δυνατό. Τι ύψος στοίβας θα βρει ο προϊστάμενος; (Α. Σολύνιν )2. Τα ύψη οξυγώνιου τριγώνου
 , στο οποίο
, στο οποίο  , τέμνονται στο σημείο
, τέμνονται στο σημείο  και
και  είναι το κέντρου του περιγεγραμμένου κύκλου του
είναι το κέντρου του περιγεγραμμένου κύκλου του  . Το τμήμα
. Το τμήμα 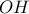 τέμνει τον περιγεγραμμένο κύκλο του τριγώνου
τέμνει τον περιγεγραμμένο κύκλο του τριγώνου  στο σημείο
στο σημείο  , διάφορο του
, διάφορο του  και
και  . Ο περιγεγραμμένος κύκλος του τριγώνου
. Ο περιγεγραμμένος κύκλος του τριγώνου  , τέμνει το έλασσον τόξο
, τέμνει το έλασσον τόξο  του κύκλου
του κύκλου  στο σημείο
στο σημείο  . Να αποδείξετε, ότι η ευθεία
. Να αποδείξετε, ότι η ευθεία  διχοτομεί το ευθύγραμμο τμήμα
διχοτομεί το ευθύγραμμο τμήμα  . (Α. Τεριέσιν)
. (Α. Τεριέσιν)3. Στον πίνακα είναι γραμμένα
 δευτεροβάθμια τριώνυμα, μεταξύ των οποίων δεν υπάρχει ζεύγος, που στο άθροισμα να δίνει μηδενικό πολυώνυμο. Προέκυψε ότι αν διαλέξουμε οποιαδήποτε δύο τριώνυμα του πίνακα
δευτεροβάθμια τριώνυμα, μεταξύ των οποίων δεν υπάρχει ζεύγος, που στο άθροισμα να δίνει μηδενικό πολυώνυμο. Προέκυψε ότι αν διαλέξουμε οποιαδήποτε δύο τριώνυμα του πίνακα  , τότε τα εναπομείναντα
, τότε τα εναπομείναντα  τριώνυμα μπορούμε να τα συμβολίσουμε
τριώνυμα μπορούμε να τα συμβολίσουμε  έτσι, ώστε όλα τα τέσσερα πολυώνυμα
έτσι, ώστε όλα τα τέσσερα πολυώνυμα  και
και  να έχουν κοινή ρίζα. Είναι άραγε απαραίτητο όλα τα τριώνυμα του πίνακα να έχουν κοινή ρίζα; (Σ. Μπερλόβ, Επιτροπή διαγωνισμού)
να έχουν κοινή ρίζα. Είναι άραγε απαραίτητο όλα τα τριώνυμα του πίνακα να έχουν κοινή ρίζα; (Σ. Μπερλόβ, Επιτροπή διαγωνισμού)4.
 παιδιά, μεταξύ των οποίων δεν υπάρχει ζεύγος ίδιου ύψους, τοποθετήθηκαν σε μια σειρά. Θα ονομάσουμε ένα ζεύγος διαφορετικών παιδιών
παιδιά, μεταξύ των οποίων δεν υπάρχει ζεύγος ίδιου ύψους, τοποθετήθηκαν σε μια σειρά. Θα ονομάσουμε ένα ζεύγος διαφορετικών παιδιών  καλό, αν μεταξύ τους δεν βρίσκεται παιδί, το ύψος του οποίου είναι μεγαλύτερο από ενός εκ των
καλό, αν μεταξύ τους δεν βρίσκεται παιδί, το ύψος του οποίου είναι μεγαλύτερο από ενός εκ των  και
και  , αλλά μικρότερο από το ύψος του άλλου. Ποιος είναι μεγαλύτερος αριθμός καλών ζευγών που μπορεί να προκύψει; (Τα ζεύγη
, αλλά μικρότερο από το ύψος του άλλου. Ποιος είναι μεγαλύτερος αριθμός καλών ζευγών που μπορεί να προκύψει; (Τα ζεύγη  και
και 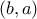 θεωρούνται το ίδιο και το αυτό ζεύγος) (Ι. Μπογκντάνοβ)
θεωρούνται το ίδιο και το αυτό ζεύγος) (Ι. Μπογκντάνοβ)