10 Μαρτίου 2024
 10η τάξη
10η τάξηΠρόβλημα 1. Η Άννα και η Ελένη παίζουν στο διάστημα
![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) , στο οποίο είναι σημειωμένα τα σημεία
, στο οποίο είναι σημειωμένα τα σημεία  και
και  . Οι παίκτριες κινούνται με την σειρά, ξεκινάει η Άννα. Με κάθε κίνηση μια παίκτρια σημειώνει ένα μη ήδη σημειωμένο σημείο του διαστήματος. Αν μετά την κίνηση της επόμενης παίκτριας βρεθούν τρία διαδοχικά διαστήματα μεταξύ γειτονικών σημειωμένων σημείων, από τα οποία μπορεί να σχηματιστεί τρίγωνο, τότε η παίκτρια που έκανε μια τέτοια κίνηση ανακοινώνεται ως νικήτρια και το παιχνίδι λήγει. Μπορεί άραγε η Άννα εγγυημένα να νικήσει; (Μπ. Μπουτίριν)
. Οι παίκτριες κινούνται με την σειρά, ξεκινάει η Άννα. Με κάθε κίνηση μια παίκτρια σημειώνει ένα μη ήδη σημειωμένο σημείο του διαστήματος. Αν μετά την κίνηση της επόμενης παίκτριας βρεθούν τρία διαδοχικά διαστήματα μεταξύ γειτονικών σημειωμένων σημείων, από τα οποία μπορεί να σχηματιστεί τρίγωνο, τότε η παίκτρια που έκανε μια τέτοια κίνηση ανακοινώνεται ως νικήτρια και το παιχνίδι λήγει. Μπορεί άραγε η Άννα εγγυημένα να νικήσει; (Μπ. Μπουτίριν)Πρόβλημα 2. Να αποδείξετε ότι μεταξύ των κορυφών ενός κυρτού εννιάγωνου μπορούν να βρεθούν τρεις, που σχηματίζουν αμβλυγώνιο τρίγωνο, καμία πλευρά του οποίου δεν συμπίπτει με τις πλευρές του εννιάγωνου. (Α. Ιουράν)
Πρόβλημα 3. Στο σύλλογο φίλων υπεργράφων στην αρχή της χρονιάς εγγράφηκαν
 ανά δυο μη γνωστοί μεταξύ τους μαθητές. Κατά την διάρκεια της χρονιάς ο σύλλογος οργάνωσε
ανά δυο μη γνωστοί μεταξύ τους μαθητές. Κατά την διάρκεια της χρονιάς ο σύλλογος οργάνωσε  συναντήσεις, εξάλλου σε κάθε συνάντηση προσήλθε τουλάχιστον ένας μαθητής. Δυο μαθητές γνωρίζονταν, αν υπήρξε έστω και μια συνάντηση στην οποία προσήλθαν και οι δυο. Στο τέλος της χρονιάς προέκυψε, ότι το πλήθος των γνωστών κάθε μαθητή είναι τουλάχιστον ίσο με το πλήθος των συναντήσεων στις οποίες προσήλθε. Να βρείτε την ελάχιστη τιμή του
συναντήσεις, εξάλλου σε κάθε συνάντηση προσήλθε τουλάχιστον ένας μαθητής. Δυο μαθητές γνωρίζονταν, αν υπήρξε έστω και μια συνάντηση στην οποία προσήλθαν και οι δυο. Στο τέλος της χρονιάς προέκυψε, ότι το πλήθος των γνωστών κάθε μαθητή είναι τουλάχιστον ίσο με το πλήθος των συναντήσεων στις οποίες προσήλθε. Να βρείτε την ελάχιστη τιμή του  , για την οποία κάτι τέτοιο μπορεί να συμβεί. (Ντ. Μετέλεβ)
, για την οποία κάτι τέτοιο μπορεί να συμβεί. (Ντ. Μετέλεβ)Πρόβλημα 4. Δίνεται ένα περιγράψιμο τετράπλευρο
 με αμβλεία την γωνία
με αμβλεία την γωνία  . Οι ημιευθείες
. Οι ημιευθείες  και
και  τέμνονται στο σημείο
τέμνονται στο σημείο  , και οι ημιευθείες
, και οι ημιευθείες  και
και  στο σημείο
στο σημείο  . Να αποδείξετε ότι
. Να αποδείξετε ότι  , όπου
, όπου  και
και 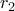 είναι τα μήκη των ακτινών των εγγεγραμμένων κύκλων των τριγώνων
είναι τα μήκη των ακτινών των εγγεγραμμένων κύκλων των τριγώνων  και
και 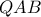 . (Λ. Σατούνοβ)
. (Λ. Σατούνοβ)Πρόβλημα 5. Θα ονομάσουμε ένα φυσικό αριθμό
 ισχυρά κυβικό, αν υπάρχει μονικό κυβικό πολυώνυμο
ισχυρά κυβικό, αν υπάρχει μονικό κυβικό πολυώνυμο  με ακέραιους συντελεστές, ώστε
με ακέραιους συντελεστές, ώστε 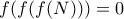 , αλλά
, αλλά  και
και 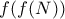 να μην είναι ίσα με
να μην είναι ίσα με  . Αληθεύει άραγε, ότι όλοι οι αριθμοί, μεγαλύτεροι του
. Αληθεύει άραγε, ότι όλοι οι αριθμοί, μεγαλύτεροι του  , είναι ισχυρά κυβικοί; (Ντ. Μπρόντσκϊι)
, είναι ισχυρά κυβικοί; (Ντ. Μπρόντσκϊι)Πρόβλημα 6. Σε κάθε μια από
 κάρτες είναι γραμμένος ένας πραγματικός αριθμός. Όλοι οι
κάρτες είναι γραμμένος ένας πραγματικός αριθμός. Όλοι οι  αριθμοί είναι διαφορετικοί και το συνολικό άθροισμά τους είναι άρρητος. Μια τράπουλα των
αριθμοί είναι διαφορετικοί και το συνολικό άθροισμά τους είναι άρρητος. Μια τράπουλα των  καρτών ονομάζεται ατυχής, αν για κάθε φυσικό αριθμό
καρτών ονομάζεται ατυχής, αν για κάθε φυσικό αριθμό  από το
από το  έως το
έως το  το άθροισμα των αριθμών των
το άθροισμα των αριθμών των  πάνω καρτών είναι άρρητο. Ο Αριστοτέλης υπολόγισε, με πόσους τρόπους μπορεί να τοποθετήσει τις αρχικές κάρτες σε ατυχή τράπουλα. Ποια είναι η ελάχιστη τιμή, που μπορεί να του προκύψει; (Α. Κουσνίρ)
πάνω καρτών είναι άρρητο. Ο Αριστοτέλης υπολόγισε, με πόσους τρόπους μπορεί να τοποθετήσει τις αρχικές κάρτες σε ατυχή τράπουλα. Ποια είναι η ελάχιστη τιμή, που μπορεί να του προκύψει; (Α. Κουσνίρ)