Μαθηματική Ολυμπιάδα Μόσχας 2024 (8η τάξη)

[Al.Koutsouridis]

LXXXVIΙ Μαθηματική Ολυμπιάδα Μόσχας
10 Μαρτίου 2024 8η τάξη

Πρόβλημα 1. Η δασκάλα υπαγόρευσε στον Τοτό την κλίση και τον σταθερό όρο τριών διαφορετικών γραμμικών συναρτήσεων, οι γραφικές παραστάσεις των οποίων είναι παράλληλες. Ο απρόσεκτος Τοτός στο γράψιμο κάθε μιας συνάρτησης αντάλλαξε την κλίση και τον σταθερό όρο και σχεδίασε την γραφική παράσταση των συναρτήσεων που προέκυψαν. Πόσα σημεία μπορεί να προέκυψαν, από τα οποία διέρχονται τουλάχιστον δυο γραφικές παραστάσεις; (Α. Πέσνιν)

Πρόβλημα 2. Στο μάθημα της φυσικής αγωγής προσήλθαν μαθητές, όλοι τους διαφορετικής δύναμης. Ο γυμναστής φορές τους χώρισε σε ομάδες των παιδιών, κάθε φορά με καινούργιο τρόπο και διεξήγαγε διελκυστίνδα μεταξύ των ομάδων. Μπορεί άραγε να προκύψει έτσι, ώστε όλες τις φορές ο αγώνας να λήξει ισόπαλος (δηλαδή το αθροίσματα των δυνάμεων των παιδιών στις ομάδες να είναι ίσα); (Μ. Ευδοκίμοβ)

Πρόβλημα 3. Το επίπεδο χωρίστηκε σε κομμάτια με μερικές ευθείες, μεταξύ των οποίων υπάρχουν μη παράλληλες. Τα κομμάτια, τα οποία το σύνορό τους αποτελείται από δυο ημιευθείες, χρωματίστηκαν. Μετά από αυτό φέρθηκε άλλη μια ευθεία. Να αποδείξετε, ότι ανεξάρτητα από την θέση της νέας ευθείας και στις δυο πλευρές της (ημιεπίπεδα που ορίζει) θα βρεθούν χρωματιστά σημεία. Παράδειγμα ευθειών (χωρίς την τελευταία ευθεία) απεικονίζεται στο σχήμα. (Α. Ούστινοβ, Α. Ιουράν)

Screenshot 2024-03-10 at 22.18.26.png (20.26 KiB) Προβλήθηκε 331 φορές

Πρόβλημα 4. Στις παράπλευρες πλευρές και ισοσκελούς οξυγώνιου τριγώνου δίνονται δυο σημεία και . Τα τμήματα 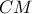και τέμνονται στο σημείο . Προέκυψε ότι . Να αποδείξετε, ότι τα μέσα όλων των δυνατών τμημάτων βρίσκονται σε μια ευθεία. (Μ. Βόλτσκεβιτς)

Πρόβλημα 5. Στη σειρά βρίσκονται κάθετα παλούκια. Σε μερικά σημεία μεταξύ γειτονικών παλουκιών βρίσκονται οριζόντια ξυλάκια, κανένα ζεύγος των οποίων δε βρίσκεται στο ίδιο ύψος. Ένα σκαθάρι κινείται από κάτω προς τα πάνω: όταν συναντάει ένα ξυλάκι, μετακινείται μέσο αυτού σε γειτονικό παλούκι και συνεχίζει να κινείται προς τα πάνω. Είναι γνωστό, ότι αν το σκαθάρι ξεκινήσει από την βάση του πρώτου παλουκιού, τότε θα τερματίσει την διαδρομή του στο ένατο παλούκι. Πάντα άραγε μπορούμε να αφαιρέσουμε ένα από τα ξυλάκια έτσι, ώστε το σκαθάρι, ξεκινώντας από την βάση του πρώτου παλουκιού, στο τέλος της διαδρομής θα βρεθεί στο άνω μέρος του πέμπτου παλουκιού;
Για παράδειγμα, αν τα ξυλάκια είναι τοποθετημένα όπως στο σχήμα, τότε το σκαθάρι θα ακολουθήσει την διαδρομή της συνεχούς γραμμής. Αν αφαιρέσουμε το τρίτο ξυλάκι στην διαδρομή του σκαθαριού, τότε θα ακολουθήσει την διαδρομή της διακεκομμένης γραμμής. (Γκ. Καραβάεβ)

Screenshot 2024-03-10 at 22.18.43.png (25.63 KiB) Προβλήθηκε 331 φορές

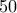Πρόβλημα 6. Ο Αλέξανδρος διάλεξε διαφορετικούς φυσικούς αριθμούς από το σύνολο και τους τοποθέτησε με κάποια σειρά στην θέση των αστεριών στην έκφραση (σύνολο αστεράκια και σύμβολα ρίζας)

.

Μπορεί άραγε η τιμή της έκφρασης να προκύψει ακέραιος αριθμός; (Μ. Ευδοκίμοβ)

[S.E.Louridas]

Πρόβλημα 4. Στις παράπλευρες πλευρές και ισοσκελούς οξυγώνιου τριγώνου δίνονται δυο σημεία και . Τα τμήματα και τέμνονται στο σημείο . Προέκυψε ότι . Να αποδείξετε, ότι τα μέσα όλων των δυνατών τμημάτων βρίσκονται σε μια ευθεία. (Μ. Βόλτσκεβιτς)

Παραθέτω το σχήμα της ημέτερης διαπραγμάτευσης με επιλεγείσα μέθοδο επίλυσης στηριζόμενη στο σημείο του Miquel.

Πράγματι επειδή το τετράπλευρο είναι εγγεγραμμένο (υπόθεση) το σημείο του Miguel (δηλαδή το κοινό σημείο των κύκλων

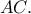είναι σημείο της ευθείας Άμεσα παίρνουμε αφενός ότι τα σημεία είναι συνευθειακά αλλά ομοίως και τα σημεία , αφετέρου ότι

τα τρίγωνα και είναι ισοσκελή. Για τα αντίστοιχα ύψη των ισοσκελών αυτών τριγώνων

προκύπτει

με και έτσι τελικά παίρνουμε ,

οπότε η απόσταση είναι σταθερή, αφού το δεξί κλάσμα αποτελείται από σταθερούς όρους.

Επομένως τα εν λόγω σημεία ανήκουν σε σταθερή παράλληλη στην ευθεία Λάβαμε υπόψη βέβαια ότι το είναι τραπέζιο και ότι

ως θεωρήσαμε το μέσο του

geometr.png (90.92 KiB) Προβλήθηκε 280 φορές

[mick7]

Για το Π1) χρησιμοποιώντας τον Desmos βρήκα 1 σημείο. Φαντάζομαι μαθηματικά παίρνεις ένα σύστημα 3 γραμμικών εξισώσεων και αφου αντιστρέψεις κλίση με σταθερό όρο δείχνεις ότι το σύστημα έχει μια λύση.

[Al.Koutsouridis]

Για το Π1) χρησιμοποιώντας τον Desmos βρήκα 1 σημείο. Φαντάζομαι μαθηματικά παίρνεις ένα σύστημα 3 γραμμικών εξισώσεων και αφου αντιστρέψεις κλίση με σταθερό όρο δείχνεις ότι το σύστημα έχει μια λύση.

Τα πράματα είναι σχετικά απλά εδώ, δεν είναι απαραίτητο να λύσει κανείς σύστημα. Αν οι τρεις ευθείες, τότε οι ευθείες, που σχεδίασε ο Τοτός είναι . Παρατηρούμε ότι για όλες τους παίρνουν την τιμή . Άρα και οι τρεις διέρχονται από το σημείο . Δηλαδή η απάντηση είναι ένα σημείο.