Τυχαίο σημείο πάνω στον περιγεγραμμένο κύκλο τριγώνου
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
-
orestisgotsis
- Δημοσιεύσεις: 1753
- Εγγραφή: Σάβ Φεβ 25, 2012 10:19 pm
Τυχαίο σημείο πάνω στον περιγεγραμμένο κύκλο τριγώνου
ΠΕΡΙΤΤΑ
τελευταία επεξεργασία από orestisgotsis σε Παρ Φεβ 23, 2024 2:18 pm, έχει επεξεργασθεί 3 φορές συνολικά.
Λέξεις Κλειδιά:
- S.E.Louridas
- Δημοσιεύσεις: 5959
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: Τυχαίο σημείο πάνω στον περιγεγραμμένο κύκλο τριγώνου
Α
Αν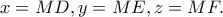 Τότε δημιουργείται η ευθεία Simson
Τότε δημιουργείται η ευθεία Simson 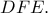
Αρκεί τελικά να αποδείξουμε οτι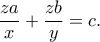
Από εύκολες ομοιότητες των τριγώνων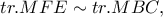 και
και 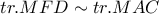 έχουμε:
έχουμε:
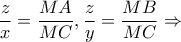
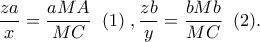
Με πρόσθεση των κατά μέλη και με βάση το Θεώρημα του Πτολεμαίου στο τετράπλευρο
κατά μέλη και με βάση το Θεώρημα του Πτολεμαίου στο τετράπλευρο 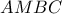 παίρνουμε το ζητούμενο.
παίρνουμε το ζητούμενο.
Επί του πιεστηριου:orestisgotsis έγραψε: ↑Τρί Ιαν 30, 2024 2:18 pmΔίνεται τρίγωνο, ο περιγεγραμμένος του κύκλος και τυχαίο σημείο
πάνω στο τόξο
του κύκλου. Αν
είναι οι αποστάσεις του
από τις πλευρές
, αντίστοιχα, να δειχθεί ότι
.
Αν
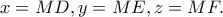 Τότε δημιουργείται η ευθεία Simson
Τότε δημιουργείται η ευθεία Simson 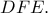
Αρκεί τελικά να αποδείξουμε οτι
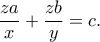
Από εύκολες ομοιότητες των τριγώνων
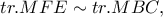 και
και 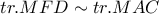 έχουμε:
έχουμε: 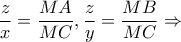
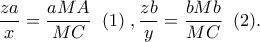
Με πρόσθεση των
 κατά μέλη και με βάση το Θεώρημα του Πτολεμαίου στο τετράπλευρο
κατά μέλη και με βάση το Θεώρημα του Πτολεμαίου στο τετράπλευρο 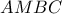 παίρνουμε το ζητούμενο.
παίρνουμε το ζητούμενο.S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13301
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Τυχαίο σημείο πάνω στον περιγεγραμμένο κύκλο τριγώνου
Ελάχιστα διαφορετικά από τον Σωτήρη.orestisgotsis έγραψε: ↑Τρί Ιαν 30, 2024 2:18 pmΣχέση αποστάσεων.png
Δίνεται τρίγωνο, ο περιγεγραμμένος του κύκλος και τυχαίο σημείο
πάνω στο τόξο
του κύκλου. Αν
είναι οι αποστάσεις του
από τις πλευρές
, αντίστοιχα, να δειχθεί ότι
.
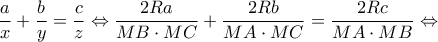
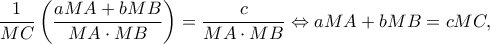
που ισχύει από το θεώρημα Πτολεμαίου στο
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 11 επισκέπτες
