Καλησπέρα καινούργιος εδώ!
Σήμερα στο Π3 της Γ Λυκείου έγραψα εν συντομία:
Ο

θα είναι της μορφής
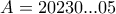
, με

μηδενικά.
Άρα θα τελειώνει σε

.
Αν ο

είναι τετράγωνο ακέραιου αριθμού, θα υπάρχει

, ώστε
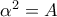
.
Απέδειξα ότι ο

θα πρέπει υποχρεωτικά να τελειώνει σε

, αφού πήρα όλους του αριθμούς από
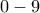
και έδειξα ότι τελειώνει σε

Έπειτα είπα ότι ο

θα έχει

τελευταία ψηφία

ή

ή
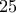
ή

ή
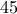
ή

ή

ή

ή

ή

.
Απέδειξα παίρνοντας όλες τις περιπτώσεις μια προς μια, ότι σε κάθε περίπτωση ο

θα τελειώνει σε
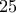
.
Αυτό όμως είναι άτοπο, αφού ο

τελειώνει σε

ή

για

.
Άρα ο

δεν υπάρχει.
Άρα ο

δεν είναι τετράγωνο ακέραιου αριθμού.
Ή απόδειξη στην κόλλα ήταν προφανώς πιο αναλυτική. Καταλαβαίνω το ότι το να παίρνεις 20 περιπτώσεις και να τις εξετάζεις μια προς μια δεν είναι κομψό. Η λύση αυτή θεωρείτε πως είναι δεκτή?
Επίσης, γνωρίζει κάποιος πόσο χρειάζεται κάποιος για να πάει στην Ευκλείδη (ή αν είναι συγκριτικό) και πότε θα βγουν τα αποτελέσματα?
(
ΣΗΜΕΙΩΣΗ ΑΠΟ ΕΠΙΜΕΛΗΤΗ (ΙΩΑΝΝΟΥ Δ.): Διόρθωσα την γραφή σε κώδικα LATEX)
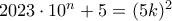
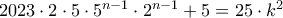
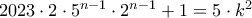

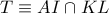 και
και 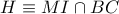
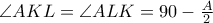 άρα
άρα 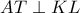
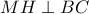 ότι ΜΘΗΔ εγγράψιμο
ότι ΜΘΗΔ εγγράψιμο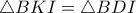 άρα
άρα 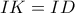
 και παραλληλα από το
και παραλληλα από το  ,
, 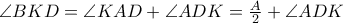
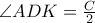 και επειδή
και επειδή 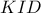 ισοσκελές,
ισοσκελές, 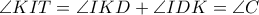
 ,
, 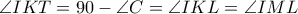
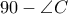 απο το ΔΘΓ, επομένως ΜΘΔΗ εγγράψιμο και εδω τελειώνει η απόδειξη
απο το ΔΘΓ, επομένως ΜΘΔΗ εγγράψιμο και εδω τελειώνει η απόδειξη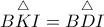 από όπου
από όπου 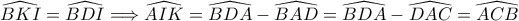 και μαζί με την παρατήρηση ότι
και μαζί με την παρατήρηση ότι 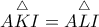 θα πάρουμε
θα πάρουμε 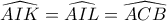 και
και 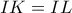 από όπου
από όπου 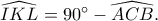 Το εγγράψιμο
Το εγγράψιμο 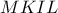 στην ουσία τελειώνει την δουλειά, αφού
στην ουσία τελειώνει την δουλειά, αφού 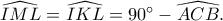
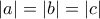 , το δεύτερο λύνεται άμεσα αν φέρεις το σύστημα στην μορφή
, το δεύτερο λύνεται άμεσα αν φέρεις το σύστημα στην μορφή 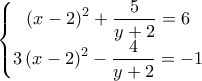 και το τέταρτο είναι μία γεωμετρία πάρα πολύ βατή. (εκφράζω την προσωπική μου άποψη). Θεωρώ ότι το 3 ήταν μακράν το πιο δύσκολο από τα 4 , λύνεται όμως με γνώσεις θεωρίας αριθμών και όταν τα πρωτοείδα τα θέματα το πρωί (έχω κάποιους μαθητές που δίνουν
και το τέταρτο είναι μία γεωμετρία πάρα πολύ βατή. (εκφράζω την προσωπική μου άποψη). Θεωρώ ότι το 3 ήταν μακράν το πιο δύσκολο από τα 4 , λύνεται όμως με γνώσεις θεωρίας αριθμών και όταν τα πρωτοείδα τα θέματα το πρωί (έχω κάποιους μαθητές που δίνουν  τότε πρέπει
τότε πρέπει 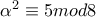
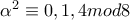
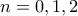
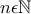 που ικανοποιεί την υπόθεση
που ικανοποιεί την υπόθεση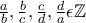 τότε
τότε 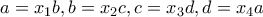
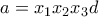
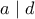 και
και 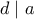
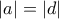
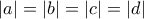
 τότε το τετράπλευρο
τότε το τετράπλευρο  είναι εγγραψίμο καθώς
είναι εγγραψίμο καθώς  .
.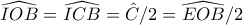 , και συνεπώς η
, και συνεπώς η 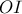 διχοτομεί τη γωνία
διχοτομεί τη γωνία  .
. είναι ισοσκελές, άρα η
είναι ισοσκελές, άρα η  .
. διχοτόμος και
διχοτόμος και  μέσο του ελάσσονος τόξου
μέσο του ελάσσονος τόξου 

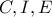 συνευθειακά. Επειδη
συνευθειακά. Επειδη 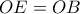 ως ακτίνες του περιγεγραμμένου του
ως ακτίνες του περιγεγραμμένου του 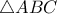 , αρκεί
, αρκεί 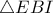 ισοσκελές. Πράγματι είναι
ισοσκελές. Πράγματι είναι 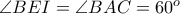 και
και 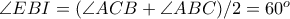
 θα είναι της μορφής
θα είναι της μορφής 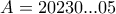 , με
, με  μηδενικά.
μηδενικά. .
.  , ώστε
, ώστε 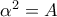 .
.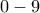 και έδειξα ότι τελειώνει σε
και έδειξα ότι τελειώνει σε 
 τελευταία ψηφία
τελευταία ψηφία  ή
ή  ή
ή 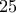 ή
ή  ή
ή 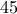 ή
ή  ή
ή  ή
ή  ή
ή  ή
ή  .
.  τελειώνει σε
τελειώνει σε  .
.  .
.  και συνεπώς το άθροισμα των αριθμών αυτών που επιλέχτηκαν είναι το πολύ
και συνεπώς το άθροισμα των αριθμών αυτών που επιλέχτηκαν είναι το πολύ 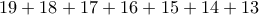 και το άθροισμα των αριθμών αυτών που δεν επιλέχτηκαν είναι τουλάχιστον
και το άθροισμα των αριθμών αυτών που δεν επιλέχτηκαν είναι τουλάχιστον 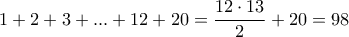 . ''
. '' 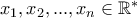 με
με 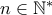
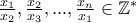 , τότε
, τότε 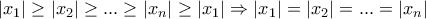
 με
με 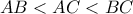 και το σημείο τομής των διχοτόμων του
και το σημείο τομής των διχοτόμων του  . Έστω ότι η ευθεία
. Έστω ότι η ευθεία  τέμνει την πλευρά
τέμνει την πλευρά  στο σημείο
στο σημείο  . Θεωρούμε σημείο
. Θεωρούμε σημείο  στην πλευρά
στην πλευρά 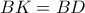 , και σημείο
, και σημείο  στην πλευρά
στην πλευρά  τέτοιο ώστε
τέτοιο ώστε 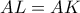 . Αν
. Αν  είναι το σημείο τομής του περιγεγραμμένου κύκλου του τριγώνου
είναι το σημείο τομής του περιγεγραμμένου κύκλου του τριγώνου  με την
με την  (διαφορετικό από το
(διαφορετικό από το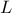 ), να αποδείξετε ότι η ευθεία
), να αποδείξετε ότι η ευθεία  είναι κάθετη στην
είναι κάθετη στην  ,
,  οι ευθείες
οι ευθείες 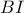 ,
,  αντίστοιχα είναι διχοτόμοι, άρα και μεσοκάθετη των τμημάτων
αντίστοιχα είναι διχοτόμοι, άρα και μεσοκάθετη των τμημάτων  ,
,  . Οπότε τα τρίγωνα
. Οπότε τα τρίγωνα  και
και 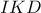 είναι ισοσκελή.
είναι ισοσκελή. 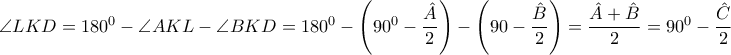 .
.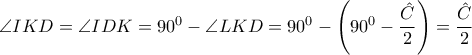 .
.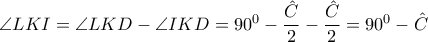 .
.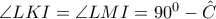 ( εγγεγραμμένες που βαίνουν στο ίδιο τόξο). Ισχύει δηλαδή ότι,
( εγγεγραμμένες που βαίνουν στο ίδιο τόξο). Ισχύει δηλαδή ότι, 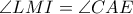 , όπου
, όπου  το ύψος του τριγώνου
το ύψος του τριγώνου 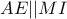 και εφόσον
και εφόσον  θα είναι και
θα είναι και  .
. , να μετατραπούν κάποια στιγμή. Η ποιότητα "ανάγνωσης" του νήματος με σχέση άλλες χρονιές είναι χειρότερη. Επίσης καλό είναι, όταν κάποιος ανοίγει το νήμα, να έχει και τα θέματα έτοιμα. Ήδη υπάρχουν 3 νήματα με τίτλο "Θαλής" 2023.
, να μετατραπούν κάποια στιγμή. Η ποιότητα "ανάγνωσης" του νήματος με σχέση άλλες χρονιές είναι χειρότερη. Επίσης καλό είναι, όταν κάποιος ανοίγει το νήμα, να έχει και τα θέματα έτοιμα. Ήδη υπάρχουν 3 νήματα με τίτλο "Θαλής" 2023. για τον οποίο να προσδιορίζεται ακέραιος
για τον οποίο να προσδιορίζεται ακέραιος  διάφορος του μηδενός τέτοιος που
διάφορος του μηδενός τέτοιος που 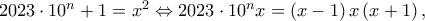 τότε το
τότε το  θα διαιρεί το δεύτερο μέλος αφού είναι γινόμενο τριών διαδοχικών ακέραιων αριθμών. Άρα ο
θα διαιρεί το δεύτερο μέλος αφού είναι γινόμενο τριών διαδοχικών ακέραιων αριθμών. Άρα ο 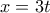 επομένως προκύπτει
επομένως προκύπτει 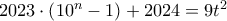 ή
ή 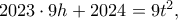 άρα θα έχουμε
άρα θα έχουμε 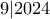 πράγμα άτοπο.
πράγμα άτοπο.