[/i]
[b]1.[/b] Σε μια σκακιέρα
 είναι τοποθετημένοι μερικοί ίπποι, εξάλλου σε κάθε τετράγωνο
είναι τοποθετημένοι μερικοί ίπποι, εξάλλου σε κάθε τετράγωνο  βρίσκεται τουλάχιστον ένας ίππος. Ποιος είναι ο ελάχιστος αριθμός κελιών που μπορούν να απειλούν αυτοί οι ίπποι; (Ο ίππος δεν απειλεί το κελί στο οποίο βρίσκεται, αλλά μπορεί να απειλεί τα κελιά στα οποία βρίσκονται άλλοι ίπποι.)
βρίσκεται τουλάχιστον ένας ίππος. Ποιος είναι ο ελάχιστος αριθμός κελιών που μπορούν να απειλούν αυτοί οι ίπποι; (Ο ίππος δεν απειλεί το κελί στο οποίο βρίσκεται, αλλά μπορεί να απειλεί τα κελιά στα οποία βρίσκονται άλλοι ίπποι.)[b]2.[/b] Δίνονται οι θετικοί ακέραιοι
 , εξάλλου
, εξάλλου  . Να αποδείξετε, ότι αν
. Να αποδείξετε, ότι αν 
τότε ο αριθμός
 είναι σύνθετος.
είναι σύνθετος.[b]3.[/b] Στον χώρο δίνονται
 σημεία, καμία τετράδα εκ των οποίων δεν είναι συνεπίπεδα. Μπορούμε να διαλέξουμε δυο σημεία
σημεία, καμία τετράδα εκ των οποίων δεν είναι συνεπίπεδα. Μπορούμε να διαλέξουμε δυο σημεία  και
και  και να μεταφέρουμε το σημείο
και να μεταφέρουμε το σημείο  στο μέσο του τμήματος
στο μέσο του τμήματος  . Προέκυψε έτσι, ώστε μετά τις μεταφορές τα σημεία έλαβαν τις ίδιες θέσεις (πιθανόν με διαφορετική σειρά). Για ποιο ελάχιστο
. Προέκυψε έτσι, ώστε μετά τις μεταφορές τα σημεία έλαβαν τις ίδιες θέσεις (πιθανόν με διαφορετική σειρά). Για ποιο ελάχιστο  αυτό είναι δυνατό;
αυτό είναι δυνατό;[b]4.[/b] Δίνονται οι θετικοί αριθμοί
 , που ικανοποιούν την συνθήκη
, που ικανοποιούν την συνθήκη .
.Να αποδείξετε την ανισότητα
 .
.[b]5.[/b] Το σημείο
 είναι το μέσο της βάσης
είναι το μέσο της βάσης  του τραπεζίου
του τραπεζίου  , εγγεγραμμένου στο κύκλο
, εγγεγραμμένου στο κύκλο  . Οι ημιευθείες
. Οι ημιευθείες  και
και  τέμνονται στο σημείο
τέμνονται στο σημείο  και η ημιευθεία
και η ημιευθεία  τέμνει τον
τέμνει τον  στο σημείο
στο σημείο  . Ο περιγεγραμμένος κύκλος του τριγώνου
. Ο περιγεγραμμένος κύκλος του τριγώνου  τέμνει την ευθεία
τέμνει την ευθεία  στο σημείο
στο σημείο  . Να αποδείξετε, ότι
. Να αποδείξετε, ότι  .
.[b]6.[/b] Από το σύνολο
 στοιχείων
στοιχείων  έχουν αφαιρεθεί μερικά υποσύνολα
έχουν αφαιρεθεί μερικά υποσύνολα  , το καθένα από τα οποία αποτελείται από τουλάχιστον δύο στοιχεία του
, το καθένα από τα οποία αποτελείται από τουλάχιστον δύο στοιχεία του  , αλλά όχι όλα. Για ποιο μέγιστο
, αλλά όχι όλα. Για ποιο μέγιστο  μπορούμε σίγουρα να γράψουμε τα στοιχεία του
μπορούμε σίγουρα να γράψουμε τα στοιχεία του  στη σειρά με τέτοια διάταξη, ώστε κανένα υποσύνολο να μην αποτελείτε από διαδοχικά στην σειρά στοιχεία;
στη σειρά με τέτοια διάταξη, ώστε κανένα υποσύνολο να μην αποτελείτε από διαδοχικά στην σειρά στοιχεία; [b]7.[/b] Ο Βασίλης σκέφτηκε ένα διψήφιο αριθμό
 και ο Πέτρος προσπαθεί να τον μαντέψει. Για τον σκοπό αυτό προφέρει έναν θετικό ακέραιο αριθμό
και ο Πέτρος προσπαθεί να τον μαντέψει. Για τον σκοπό αυτό προφέρει έναν θετικό ακέραιο αριθμό  και ο Βασίλης ανακοινώνει στον Πέτρο το άθροισμα των ψηφίων του αριθμού
και ο Βασίλης ανακοινώνει στον Πέτρο το άθροισμα των ψηφίων του αριθμού  . Για ποιο ελάχιστο αριθμό τέτοιων πράξεων ο Πέτρος εγγυημένα μπορεί να προσδιορίσει τον αριθμό του Βασίλη;
. Για ποιο ελάχιστο αριθμό τέτοιων πράξεων ο Πέτρος εγγυημένα μπορεί να προσδιορίσει τον αριθμό του Βασίλη;[b]8.[/b] Θα λέμε ότι, μια τριγωνική πυραμίδα διαμερίζει ένα παραλληλεπίπεδο, αν το παραλληλεπίπεδο μπορεί να διαμεριστεί σε
 αντίγραφα αυτής της τριγωνικής πυραμίδας. Υπάρχει άραγε παραλληλεπίπεδο, το οποίο το διαμερίζουν τουλάχιστον δυο διαφορετικές τριγωνικές πυραμίδες;
αντίγραφα αυτής της τριγωνικής πυραμίδας. Υπάρχει άραγε παραλληλεπίπεδο, το οποίο το διαμερίζουν τουλάχιστον δυο διαφορετικές τριγωνικές πυραμίδες;[url=http://www.239.ru/node/1838][color=#000080][size=85]Πηγή[/size][/color][/url]

 είναι θετικός ακέραιος, έτσι πρέπει και το
είναι θετικός ακέραιος, έτσι πρέπει και το  . Τότε
. Τότε .
. τώρα θα είναι
τώρα θα είναι


 , άτοπο από την αρχική, και το ζητούμενο έπεται.
, άτοπο από την αρχική, και το ζητούμενο έπεται. , ανεξάρτητα αν και αυτή οδηγεί εύκολα σε άτοπο.
, ανεξάρτητα αν και αυτή οδηγεί εύκολα σε άτοπο. προφανές άτοπο, αλλά όντως θα έπρεπε να το γράψω...
προφανές άτοπο, αλλά όντως θα έπρεπε να το γράψω... ή όχι. Πάλι εύκολα οδηγούμαστε σε άτοπο, αλλά δεν είναι φανερό από το παραπάνω βήμα ή στην αρχική λύση αν εξετάστηκε. Το έγραψα περισσότερο, σε πραγματική εξέταση να μην χάνουμε "χαζά" μόρια.
ή όχι. Πάλι εύκολα οδηγούμαστε σε άτοπο, αλλά δεν είναι φανερό από το παραπάνω βήμα ή στην αρχική λύση αν εξετάστηκε. Το έγραψα περισσότερο, σε πραγματική εξέταση να μην χάνουμε "χαζά" μόρια. τέμνει το μεγάλο κύκλο στο
τέμνει το μεγάλο κύκλο στο 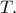 Αρχικά θα δείξω ότι τα σημεία
Αρχικά θα δείξω ότι τα σημεία  είναι συνευθειακά.
είναι συνευθειακά.  άρα το
άρα το  είναι εγγράψιμο, οπότε:
είναι εγγράψιμο, οπότε: άρα τα
άρα τα  είναι το ύψος του τριγώνου
είναι το ύψος του τριγώνου  κι επειδή
κι επειδή  θα είναι
θα είναι 
 , ή ισοδύναμα
, ή ισοδύναμα  (πολλαπλασιάζοντας αριθμητή και παρονομαστή κάθε κλάσματος με
(πολλαπλασιάζοντας αριθμητή και παρονομαστή κάθε κλάσματος με 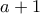 ,
,  κτλ).
κτλ). , δηλαδή ότι
, δηλαδή ότι  .
. , οπότε
, οπότε  , και αρκεί να αποδείξουμε ότι
, και αρκεί να αποδείξουμε ότι ![\displaystyle{\sum x\sqrt[3]{(\dfrac{1}{x}-1)^2} \leq 2} \displaystyle{\sum x\sqrt[3]{(\dfrac{1}{x}-1)^2} \leq 2}](/forum/ext/geomar/texintegr/latexrender/pictures/57ca1c504f0b87711a3a58f1c61d7669.png) , ή ισοδύναμα ότι
, ή ισοδύναμα ότι ![\displaystyle{\sum \sqrt[3]{x(1-x)^2} \leq 2} \displaystyle{\sum \sqrt[3]{x(1-x)^2} \leq 2}](/forum/ext/geomar/texintegr/latexrender/pictures/ceb751b9ca7aa539830c07df62280fe0.png) .
.![\sqrt[3]{x(1-x)^2} \leq \sqrt[3]{\dfrac{1-x}{4}} \sqrt[3]{x(1-x)^2} \leq \sqrt[3]{\dfrac{1-x}{4}}](/forum/ext/geomar/texintegr/latexrender/pictures/b1e3032de0eaef4513026738c9c8cd79.png) , οπότε
, οπότε ![\displaystyle{\sum \sqrt[3]{x(1-x)^2} \leq \dfrac{1}{\sqrt[3]{4}}\sum \sqrt[3]{1-x}} \displaystyle{\sum \sqrt[3]{x(1-x)^2} \leq \dfrac{1}{\sqrt[3]{4}}\sum \sqrt[3]{1-x}}](/forum/ext/geomar/texintegr/latexrender/pictures/6c41dd237faa82b39c5d716fe772559c.png) .
.![\displaystyle{ \sum \sqrt[3]{1-x} \leq \sqrt[3]{16\sum (1-x)}=\sqrt[3]{32}} \displaystyle{ \sum \sqrt[3]{1-x} \leq \sqrt[3]{16\sum (1-x)}=\sqrt[3]{32}}](/forum/ext/geomar/texintegr/latexrender/pictures/3ebac3d0a27d922f64ce753895d48897.png) , οπότε και
, οπότε και ![\displaystyle{\sum \sqrt[3]{x(1-x)^2} \leq \dfrac{1}{\sqrt[3]{4}}\sum \sqrt[3]{1-x} \leq \sqrt[3]{8}=2} \displaystyle{\sum \sqrt[3]{x(1-x)^2} \leq \dfrac{1}{\sqrt[3]{4}}\sum \sqrt[3]{1-x} \leq \sqrt[3]{8}=2}](/forum/ext/geomar/texintegr/latexrender/pictures/9d2b619f332bb562068a3ba5ce072c03.png) , και η απόδειξη ολοκληρώθηκε.
, και η απόδειξη ολοκληρώθηκε. , δηλαδή όταν
, δηλαδή όταν  .
.