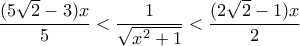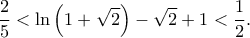
Μία ενδιαφέρουσα ανισότητα!
Συντονιστής: Μπάμπης Στεργίου
Re: Μία ενδιαφέρουσα ανισότητα!
Ισοδύναμα : 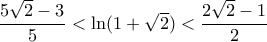 .
.
Αλλά :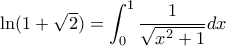 .
.
Αφήνω την σκέψη για πιθανή αξιοποίηση , διότι η διπλή ανισότητα που είχα γράψει
δεν ισχύει , όπως έγραψε ο Μιχάλης παρακάτω
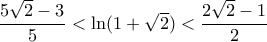 .
. Αλλά :
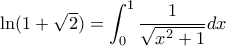 .
. Αφήνω την σκέψη για πιθανή αξιοποίηση , διότι η διπλή ανισότητα που είχα γράψει
δεν ισχύει , όπως έγραψε ο Μιχάλης παρακάτω
τελευταία επεξεργασία από KARKAR σε Τρί Ιαν 09, 2024 7:11 am, έχει επεξεργασθεί 1 φορά συνολικά.
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15768
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Μία ενδιαφέρουσα ανισότητα!
Θανάση, στην δεξιά κάποιο τυπογραφικό σφάλμα θα έχεις: Παίρνοντας όριο
 δίνει
δίνει 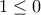 .
.Re: Μία ενδιαφέρουσα ανισότητα!
λαθος πραξεις συγνωμη
τελευταία επεξεργασία από R BORIS σε Τρί Ιαν 16, 2024 8:09 am, έχει επεξεργασθεί 1 φορά συνολικά.
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3345
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Μία ενδιαφέρουσα ανισότητα!
Επειδή υπάρχουν σοβαρά προβλήματα στην ως άνω προσέγγιση, το προχωρώ χωρίς Λογισμό, με χρήση όμως των 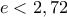 και
και 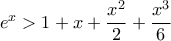 :
:
H δεξιά ανισότητα γράφεται ως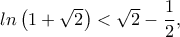 ισοδύναμα
ισοδύναμα 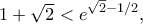 άρα αρκεί να δειχθεί η
άρα αρκεί να δειχθεί η 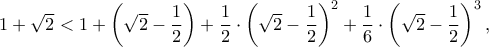 ισοδύναμη τελικά προς την
ισοδύναμη τελικά προς την 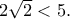
Η αριστερή ανισότητα γράφεται ως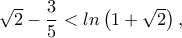 και επειδή
και επειδή 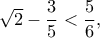 αρκεί να παρατηρηθεί ότι
αρκεί να παρατηρηθεί ότι 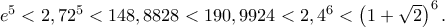
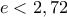 και
και 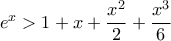 :
:H δεξιά ανισότητα γράφεται ως
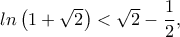 ισοδύναμα
ισοδύναμα 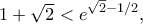 άρα αρκεί να δειχθεί η
άρα αρκεί να δειχθεί η 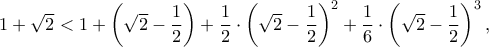 ισοδύναμη τελικά προς την
ισοδύναμη τελικά προς την 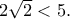
Η αριστερή ανισότητα γράφεται ως
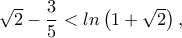 και επειδή
και επειδή 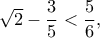 αρκεί να παρατηρηθεί ότι
αρκεί να παρατηρηθεί ότι 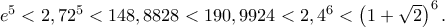
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Re: Μία ενδιαφέρουσα ανισότητα!
Για την αριστερή ανισότητα , μπορούμε να πετύχουμε ουσιωδώς καλύτερη προσέγγιση .
Η ευθεία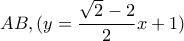 , βρίσκεται κάτω από την γραφική παράσταση της
, βρίσκεται κάτω από την γραφική παράσταση της  ,
,
( εκτός των άκρων Α , Β ) , συνεπώς ( τραπέζιο ) :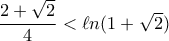 .
.
Εύκολα τώρα είναι :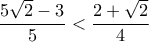 , ( είναι ισοδύναμη με την :
, ( είναι ισοδύναμη με την : 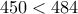 ) .
) .
Η ευθεία
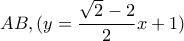 , βρίσκεται κάτω από την γραφική παράσταση της
, βρίσκεται κάτω από την γραφική παράσταση της  ,
,( εκτός των άκρων Α , Β ) , συνεπώς ( τραπέζιο ) :
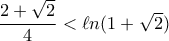 .
.Εύκολα τώρα είναι :
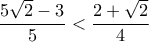 , ( είναι ισοδύναμη με την :
, ( είναι ισοδύναμη με την : 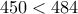 ) .
) .- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3345
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Μία ενδιαφέρουσα ανισότητα!
Θανάση πολύ ωραία, για την δεξιά ανισότητα ... μπορούμε επίσης να φέρουμε την εφαπτομενη στο
 , παραμενουσα πάνω από την κοιλη στο
, παραμενουσα πάνω από την κοιλη στο  συνάρτηση
συνάρτηση  , η οποία τέμνει τις ευθείες
, η οποία τέμνει τις ευθείες  και
και  για
για 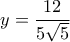 και
και 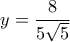 , αντίστοιχα, και όλα αυτά οδηγούν στην βελτιωμένη προσέγγιση
, αντίστοιχα, και όλα αυτά οδηγούν στην βελτιωμένη προσέγγιση 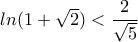 , κλπ
, κλπ[Προσθέτω ότι αυτή συμβαίνει να είναι και η καλύτερη άνω προσέγγιση με την συγκεκριμένη μέθοδο, καθώς... φέρνοντας την εφαπτομενη στο
 προκύπτει εμβαδόν τραπεζίου ίσο προς
προκύπτει εμβαδόν τραπεζίου ίσο προς 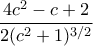 , κλπ]
, κλπ]Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Re: Μία ενδιαφέρουσα ανισότητα!
Η 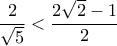 , ισοδυναμεί με την
, ισοδυναμεί με την 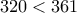 , που φυσικά ισχύει .
, που φυσικά ισχύει .
Συνοπτικά έχουμε :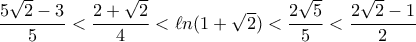 .
.
Με προσεγγίσεις στο τέταρτο δεκαδικό , είναι :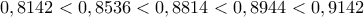
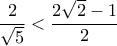 , ισοδυναμεί με την
, ισοδυναμεί με την 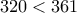 , που φυσικά ισχύει .
, που φυσικά ισχύει .Συνοπτικά έχουμε :
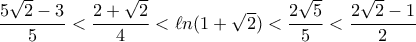 .
.Με προσεγγίσεις στο τέταρτο δεκαδικό , είναι :
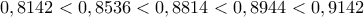
Re: Μία ενδιαφέρουσα ανισότητα!
Στην προσπάθεια να "πιάσουμε" την σκέψη του θεματοδότη : Είναι :
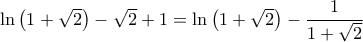
Η συνάρτηση :
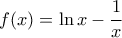 , είναι γνησίως αύξουσα στους θετικούς ,
, είναι γνησίως αύξουσα στους θετικούς , συνεπώς επειδή :
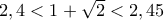 , αρκεί να δείξω ότι :
, αρκεί να δείξω ότι : 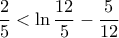 και :
και : 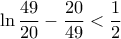 .
.Αυτές γίνονται :
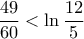 και :
και : 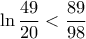 . Ισχύουν αφού :
. Ισχύουν αφού :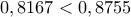 και :
και : 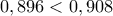 , αλλά δεν βλέπω εύκολη απόδειξη ...
, αλλά δεν βλέπω εύκολη απόδειξη ...Re: Μία ενδιαφέρουσα ανισότητα!
Ωραία...μια απόδειξη της 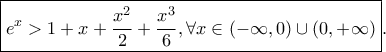 Θεωρούμε την δύο φορές παραγωγίσιμη συνάρτηση
Θεωρούμε την δύο φορές παραγωγίσιμη συνάρτηση 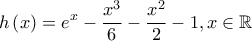 με
με 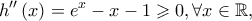 με την ισότητα μόνο για
με την ισότητα μόνο για  Άρα η
Άρα η  είναι κυρτή στο
είναι κυρτή στο  και η εξίσωση εφαπτομένης της
και η εξίσωση εφαπτομένης της 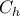 στο σημείο της
στο σημείο της 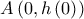 είναι
είναι 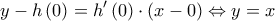 , άρα
, άρα 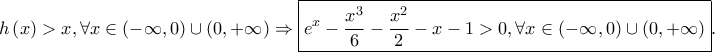
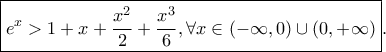 Θεωρούμε την δύο φορές παραγωγίσιμη συνάρτηση
Θεωρούμε την δύο φορές παραγωγίσιμη συνάρτηση 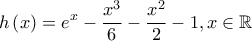 με
με 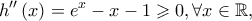 με την ισότητα μόνο για
με την ισότητα μόνο για  Άρα η
Άρα η  είναι κυρτή στο
είναι κυρτή στο  και η εξίσωση εφαπτομένης της
και η εξίσωση εφαπτομένης της 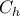 στο σημείο της
στο σημείο της 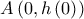 είναι
είναι 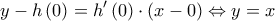 , άρα
, άρα 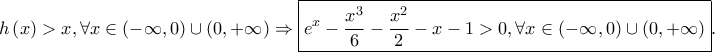
-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: Μία ενδιαφέρουσα ανισότητα!
Υπάρχει τυπογραφικό.
Είναι
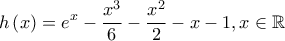
Τέτοιου είδους ανισότητες αποδεικνύονται πιο εύκολα αν θεωρήσουμε την
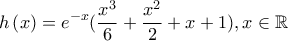
Δυο κουβέντες για την αρχική ανισότητα.
Μπορεί εύκολα με παραγώγους να δειχθεί ότι
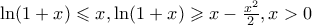
Γράφοντας
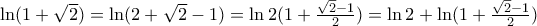
και εφαρμόζοντας την προηγούμενη βγαίνει.
Re: Μία ενδιαφέρουσα ανισότητα!
Ας νου επιτραπεί να ζητήσω από τον θεματοδότη αναλυτικότερη παρουσίαση της λύσης 
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες

 , να ισχύει :
, να ισχύει :