 μια δύο φορές παραγωγίσιμη συνάρτηση με συνεχή δεύτερη παράγωγο , για την οποία ισχύουν:
μια δύο φορές παραγωγίσιμη συνάρτηση με συνεχή δεύτερη παράγωγο , για την οποία ισχύουν:

 και
και 
(α) Να αποδείξετε ότι η
 είναι κοίλη.
είναι κοίλη.(β) Να λύσετε την ανίσωση

(γ) Να βρείτε τα κοινά σημεία των γραφικών παραστάσεων των συναρτήσεων
 και
και 
Συντονιστής: Καρδαμίτσης Σπύρος
 μια δύο φορές παραγωγίσιμη συνάρτηση με συνεχή δεύτερη παράγωγο , για την οποία ισχύουν:
μια δύο φορές παραγωγίσιμη συνάρτηση με συνεχή δεύτερη παράγωγο , για την οποία ισχύουν:

 και
και 
 είναι κοίλη.
είναι κοίλη.
 και
και 
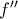 και το γεγονός ότι δεν μηδενίζεται πουθενά στο
και το γεγονός ότι δεν μηδενίζεται πουθενά στο  μας δίνει ότι διατηρεί πρόσημο.
μας δίνει ότι διατηρεί πρόσημο. είναι είτε κυρτή ή κοίλη. Ας υποθέσουμε, προς άτοπο, ότι η
είναι είτε κυρτή ή κοίλη. Ας υποθέσουμε, προς άτοπο, ότι η  είναι κυρτή. Τότε η γραφική της παράσταση θα είναι πάνω από την
είναι κυρτή. Τότε η γραφική της παράσταση θα είναι πάνω από την  , οπότε
, οπότε 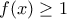 για όλα τα
για όλα τα  Ωστόσο, λόγω συνέχειας στο
Ωστόσο, λόγω συνέχειας στο  και εκμεταλλευόμενοι το όριο βρίσκουμε
και εκμεταλλευόμενοι το όριο βρίσκουμε![\displaystyle{0=\lim_{x\to 0}\frac{f(x)\,\eta \mu\,x+\sigma \upsilon \nu\,x-1}{x}=\lim_{x\to 0}\left[f(x)\,\frac{\eta \mu\,x}{x}+\frac{\sigma \upsilon \nu\,x-1}{x}\right]=f(0)\cdot 1+0=f(0)} \displaystyle{0=\lim_{x\to 0}\frac{f(x)\,\eta \mu\,x+\sigma \upsilon \nu\,x-1}{x}=\lim_{x\to 0}\left[f(x)\,\frac{\eta \mu\,x}{x}+\frac{\sigma \upsilon \nu\,x-1}{x}\right]=f(0)\cdot 1+0=f(0)}](/forum/ext/geomar/texintegr/latexrender/pictures/4644eaddb93731c1f59ac585b519f708.png)
 κοίλη στο
κοίλη στο 
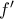 είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο  με μοναδική ρίζα το
με μοναδική ρίζα το  . Άρα
. Άρα  που σημαίνει ότι η
που σημαίνει ότι η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο  , είναι
, είναι![\left(-\infty,1\right] \left(-\infty,1\right]](/forum/ext/geomar/texintegr/latexrender/pictures/d91f4dbea4095389981aba396d58247d.png) και παρουσιάζει μοναδικό (ολικό μέγιστο) ακρότατο στο
και παρουσιάζει μοναδικό (ολικό μέγιστο) ακρότατο στο  .
.  έχουμε
έχουμε
 για όλα τα
για όλα τα  με ισότητα να πιάνεται μόνο για
με ισότητα να πιάνεται μόνο για 
 η οποία είναι δύο φορές συνεχώς παραγωγίσιμη με
η οποία είναι δύο φορές συνεχώς παραγωγίσιμη με 
 έχει το πολύ δύο ρίζες. Προφανείς ωστόσο είναι οι
έχει το πολύ δύο ρίζες. Προφανείς ωστόσο είναι οι 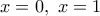 και άρα δύο ακριβώς ρίζες
και άρα δύο ακριβώς ρίζες  . Γεωμετρικά οι
. Γεωμετρικά οι  τέμνονται ακριβώς σε δύο σημεία.
τέμνονται ακριβώς σε δύο σημεία. είναι συνεχής στο
είναι συνεχής στο  άρα
άρα  και αφού
και αφού  άρα
άρα ![\displaystyle \lim_{x\rightarrow 0}\left [ f\left ( x \right )\cdot \frac{\eta \mu x}{x}+\frac{\sigma \upsilon \nu x-1}{x} \right ]=f\left ( 0 \right )+0=0\Rightarrow f\left ( 0 \right )=0. \displaystyle \lim_{x\rightarrow 0}\left [ f\left ( x \right )\cdot \frac{\eta \mu x}{x}+\frac{\sigma \upsilon \nu x-1}{x} \right ]=f\left ( 0 \right )+0=0\Rightarrow f\left ( 0 \right )=0.](/forum/ext/geomar/texintegr/latexrender/pictures/4ec50a30ebf288258d06fc9d821ed0e9.png) Η
Η  είναι συνεχής στο
είναι συνεχής στο ![\left [ 0,1 \right ] \left [ 0,1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/0484f17e7cb175ea6829cc0e1ad3d5a5.png) και παραγωγίσιμη στο
και παραγωγίσιμη στο  άρα από ΘΜΤ υπάρχει
άρα από ΘΜΤ υπάρχει 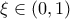 με
με  και
και  άρα η
άρα η  δεν είναι αύξουσα στο
δεν είναι αύξουσα στο  . Η
. Η 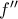 είναι συνεχής στο
είναι συνεχής στο  και δεν έχει πραγματικές ρίζες, άρα από τις συνέπειες του Θ. Bolzano η
και δεν έχει πραγματικές ρίζες, άρα από τις συνέπειες του Θ. Bolzano η 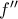 διατηρεί πρόσημο στο
διατηρεί πρόσημο στο  , άρα η
, άρα η  είναι γνησίως μονότονη και αφού δεν είναι αύξουσα, άρα είναι γνησίως φθίνουσα και η
είναι γνησίως μονότονη και αφού δεν είναι αύξουσα, άρα είναι γνησίως φθίνουσα και η  είναι κοίλη.
είναι κοίλη.  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο  και η ανίσωση που είναι
και η ανίσωση που είναι  γίνεται
γίνεται  Η εξίσωση εφαπτομένης της
Η εξίσωση εφαπτομένης της  στο σημείο της
στο σημείο της  είναι
είναι  και η
και η  είναι κοίλη στο
είναι κοίλη στο  άρα
άρα  με την ισότητα μόνο για
με την ισότητα μόνο για  και συνεπώς η ανίσωση έχει μόνη λύση την
και συνεπώς η ανίσωση έχει μόνη λύση την 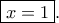
 Η
Η  είναι παραγωγίσιμη με
είναι παραγωγίσιμη με  Αφού η
Αφού η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο  ισχύουν οι ισοδυαναμίες:
ισχύουν οι ισοδυαναμίες: 


 είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο ![\left ( -\infty,\xi \right ] \left ( -\infty,\xi \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/b83140950652060c30bf80b7dbc0d513.png) και γνησίως φθίνουσα στο
και γνησίως φθίνουσα στο  άρα η
άρα η  έχει το πολύ δύο ρίζες στο
έχει το πολύ δύο ρίζες στο  Όμως
Όμως  άρα η
άρα η  έχει μοναδικές ρίζες τις
έχει μοναδικές ρίζες τις  και
και 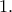 Τα ζητούμενα σημεία είναι τα
Τα ζητούμενα σημεία είναι τα  και
και 
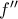 διατηρεί πρόσημο στο
διατηρεί πρόσημο στο  δεν χρειάζεται η συνέχεια της δεύτερης παραγώγου. Είναι η συνέπεια του Θ. Darboux. Αλλά για Γ λυκείου το έδωσα έτσι.
δεν χρειάζεται η συνέχεια της δεύτερης παραγώγου. Είναι η συνέπεια του Θ. Darboux. Αλλά για Γ λυκείου το έδωσα έτσι.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες