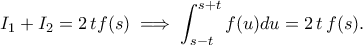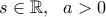 και η δύο φορές παραγωγίσιμη συνάρτηση
και η δύο φορές παραγωγίσιμη συνάρτηση ![\displaystyle{f:[s-a,s+a]\to \mathbb{R}}} \displaystyle{f:[s-a,s+a]\to \mathbb{R}}}](/forum/ext/geomar/texintegr/latexrender/pictures/c5806c360c71a6e97f43dc65430339cb.png) ,
, για την οποία γνωρίζουμε ότι:
- η
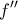 είναι συνεχής και έχει μοναδική ρίζα στο
είναι συνεχής και έχει μοναδική ρίζα στο 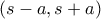
Ι1.Η συνάρτηση
 με
με  είναι περιττή.
είναι περιττή.Ι2. Το συμμετρικό του σημείου
 της
της  ως προς το
ως προς το 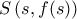 είναι σημείο της
είναι σημείο της  . Η
. Η  έχει κέντρο συμμετρίας το
έχει κέντρο συμμετρίας το 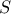 .
.Ι3. Το σημείο
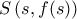 είναι το μοναδικό σημείο καμπής της
είναι το μοναδικό σημείο καμπής της  .
.Ι4.
 διαφορετικά συμμετρικά σημεία της
διαφορετικά συμμετρικά σημεία της  αν και μόνο αν οι εφαπτομένες της
αν και μόνο αν οι εφαπτομένες της  στα
στα  είναι παράλληλες.
είναι παράλληλες.Ι5. Αν
 δύο διαφορετικά συμμετρικά σημεία της
δύο διαφορετικά συμμετρικά σημεία της  τότε υπάρχουν δύο ακριβώς εφαπτομένες της
τότε υπάρχουν δύο ακριβώς εφαπτομένες της  παράλληλες στην ευθεία
παράλληλες στην ευθεία  .
.Ι6. Αν η
 έχει τοπικό μέγιστο σε σημείο του διαστήματος
έχει τοπικό μέγιστο σε σημείο του διαστήματος 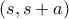 το
το 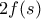 και
και 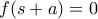 ,
, το σύνολο τιμών της
 είναι το
είναι το ![\displaystyle{[0,2f(s)]} \displaystyle{[0,2f(s)]}](/forum/ext/geomar/texintegr/latexrender/pictures/894426412ce9860af1788276e28cd887.png) .
.Ι7. Αν η
 δεν έχει τοπικό ακρότατο στο
δεν έχει τοπικό ακρότατο στο 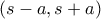 , τότε είναι γνησίως μονότονη.
, τότε είναι γνησίως μονότονη.Ι8.
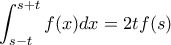 , με
, με ![\displaystyle{t\in[0,a]} \displaystyle{t\in[0,a]}](/forum/ext/geomar/texintegr/latexrender/pictures/85305e285426e2c0389b23ed9955f2ca.png)
Ι9. Αν η συνάρτηση
 δεν έχει τοπικό ακρότατο στο
δεν έχει τοπικό ακρότατο στο 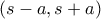
- α) Υπάρχει
 ώστε το σύνολο τιμών της
ώστε το σύνολο τιμών της  να είναι συμμετρικό ως προς το
να είναι συμμετρικό ως προς το  . Δηλαδή
. Δηλαδή ![\displaystyle{f(A)= [f(s)-b,f(s)+b]} \displaystyle{f(A)= [f(s)-b,f(s)+b]}](/forum/ext/geomar/texintegr/latexrender/pictures/b93db7a72a9e52cf31c1fbf4eb24239c.png) .
.
- β) Η αντίστροφη της
 είναι συμμετρική: Ισχύει
είναι συμμετρική: Ισχύει ![\displaystyle{f^{-1}\left(f(s)-y\right)+f^{-1}\left(f(s)+y\right)=2s, \ \ \forall y \in [0,b]} \displaystyle{f^{-1}\left(f(s)-y\right)+f^{-1}\left(f(s)+y\right)=2s, \ \ \forall y \in [0,b]}](/forum/ext/geomar/texintegr/latexrender/pictures/6972821b8ef5063cbc759685efd7a322.png) .
.
Edit 14/12/2023 17.30: Συμπλήρωσα το Ι9.

![\displaystyle{\boxed{f(s-x)+f(s+x)=2f(s), \ \ \forall x \in [0,a]} \bf(1)} \displaystyle{\boxed{f(s-x)+f(s+x)=2f(s), \ \ \forall x \in [0,a]} \bf(1)}](/forum/ext/geomar/texintegr/latexrender/pictures/c450b7bd006b52f0c9290e63e1ea4ee6.png)


![\left[-a,a\right]. \left[-a,a\right].](/forum/ext/geomar/texintegr/latexrender/pictures/8f954b9ac10b1f4582fb276cfed887d6.png)
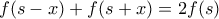 ισχύει και
ισχύει και ![\displaystyle{\forall x\in [-a,0]} \displaystyle{\forall x\in [-a,0]}](/forum/ext/geomar/texintegr/latexrender/pictures/e0e4f93e9f4ef899754e9ae2ac086174.png) αφού
αφού ![\displaystyle{-x\in [0,a]} \displaystyle{-x\in [0,a]}](/forum/ext/geomar/texintegr/latexrender/pictures/c404c2709e2382ab2f923afa7e8779cd.png) οπότε
οπότε 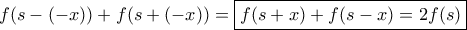
 ορίζεται στο συμμετρικό περί του
ορίζεται στο συμμετρικό περί του  διάστημα
διάστημα ![\left[-a,a\right] \left[-a,a\right]](/forum/ext/geomar/texintegr/latexrender/pictures/a4e28525019c370bbf7e1e8343dea868.png) και έχουμε
και έχουμε ![\displaystyle{g(-x)=f(s-x)-f(s)\stackrel{(1)}{=}f(s)-f(s+x)=-g(x),\,\,\forall\,x\in\left[-a,a\right].} \displaystyle{g(-x)=f(s-x)-f(s)\stackrel{(1)}{=}f(s)-f(s+x)=-g(x),\,\,\forall\,x\in\left[-a,a\right].}](/forum/ext/geomar/texintegr/latexrender/pictures/ba5b254e54bed925d6c195cd65465219.png)
![N(z,w),\,z\in\left[s-a,s+a\right], N(z,w),\,z\in\left[s-a,s+a\right],](/forum/ext/geomar/texintegr/latexrender/pictures/5263c3c22c5d945abfca2b4130d23741.png) το συμμετρικό του
το συμμετρικό του 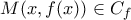 ως προς τo
ως προς τo 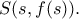 Τότε έχουμε
Τότε έχουμε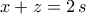 καθώς και
καθώς και 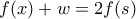 , οπότε προκύπτει ότι
, οπότε προκύπτει ότι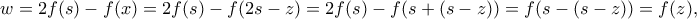 οπότε
οπότε 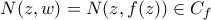
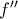 είναι συνεχής με μοναδική ρίζα, έστω
είναι συνεχής με μοναδική ρίζα, έστω 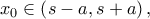 διατηρεί σταθερό πρόσημο στα
διατηρεί σταθερό πρόσημο στα 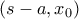 και
και 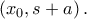
 έχει καμπή. Δε μπορεί να έχει σε άλλο σημείο
έχει καμπή. Δε μπορεί να έχει σε άλλο σημείο 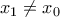 διότι από γνωστό θεώρημα
διότι από γνωστό θεώρημα 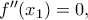 άτοπο.
άτοπο.![f^{\prime \prime}(s+x)+f^{\prime \prime}(s-x)=0,\,\,x\in\left[0,a\right] f^{\prime \prime}(s+x)+f^{\prime \prime}(s-x)=0,\,\,x\in\left[0,a\right]](/forum/ext/geomar/texintegr/latexrender/pictures/f39d852a163cc1066c7467f81787142c.png) όπου για
όπου για  προκύπτει
προκύπτει
![t\in\left[0,a\right]. t\in\left[0,a\right].](/forum/ext/geomar/texintegr/latexrender/pictures/e200941ab901744f3b542ca4ab4fd86b.png) Θέτουμε
Θέτουμε 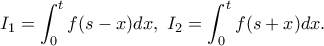
 κάνουμε αντικατάσταση
κάνουμε αντικατάσταση 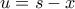 ενώ στο ολοκλήρωμα
ενώ στο ολοκλήρωμα  κάνουμε αντικατάσταση
κάνουμε αντικατάσταση 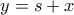 και προκύπτουν:
και προκύπτουν: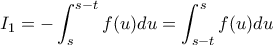 και
και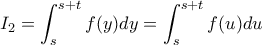
![\left[0,t\right] \left[0,t\right]](/forum/ext/geomar/texintegr/latexrender/pictures/da5001a573772aa44c4beaae88c2acb1.png) έχουμε
έχουμε