ΘΕΜΑ 1
Συντονιστής: Καρδαμίτσης Σπύρος
-
orestisgotsis
- Δημοσιεύσεις: 1753
- Εγγραφή: Σάβ Φεβ 25, 2012 10:19 pm
ΘΕΜΑ 1
ΠΕΡΙΤΤΑ
τελευταία επεξεργασία από orestisgotsis σε Κυρ Φεβ 25, 2024 12:37 am, έχει επεξεργασθεί 1 φορά συνολικά.
Λέξεις Κλειδιά:
- Maria-Eleni Nikolaou
- Δημοσιεύσεις: 82
- Εγγραφή: Δευ Σεπ 27, 2021 8:14 pm
- Τοποθεσία: Άγιοι Απόστολοι - Κάλαμος Αττικής
Re: ΘΕΜΑ 1
orestisgotsis έγραψε: ↑Πέμ Μάιος 11, 2023 6:20 pmΔίνεται η συνάρτηση, όπου α θετικός πραγματικός αριθμός με
.
α) Να βρεθεί ο α ώστε η συνάρτησηνα παρουσιάζει ελάχιστο.
β) Για οποιαδήποτε από τις τιμές του α που βρήκατε στο (α) ερώτημα, αποδείξτε ότι
για την παραπάνω συνάρτησηισχύει ότι το εμβαδό του χωρίου που περικλείεται
από τηνκαι τον άξονα
δεν είναι μεγαλύτερο από
τ.μ.
 Έστω
Έστω 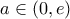 , τότε:
, τότε:![\displaystyle f(x)=\lim_{y\to +\infty} \dfrac{e^y[x\cdot {(\frac{a}{e})}^y +x^2-1]}{e^{y-1}[ {(\frac{a}{e})}^{y-1} +e^4]} = \dfrac{e(x^2-1)}{e^4} = \dfrac{x^2-1}{e^3} \displaystyle f(x)=\lim_{y\to +\infty} \dfrac{e^y[x\cdot {(\frac{a}{e})}^y +x^2-1]}{e^{y-1}[ {(\frac{a}{e})}^{y-1} +e^4]} = \dfrac{e(x^2-1)}{e^4} = \dfrac{x^2-1}{e^3}](/forum/ext/geomar/texintegr/latexrender/pictures/2b326effc3962ae842eeb3fa6468b557.png)
Οπότε,
 . Για να παρουσιάζει η
. Για να παρουσιάζει η  ελάχιστο, πρέπει
ελάχιστο, πρέπει 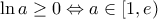
Τότε,
![\displaystyle E= -\int_{-1}^{1}g(x)dx=\int_{-1}^{1}\ln a(1-x^2)dx=\ln a\left [ x-\dfrac{x^3}{3} \right ]_{-1}^{1}=\dfrac{4}{3}\ln a<\frac{4}{3} \displaystyle E= -\int_{-1}^{1}g(x)dx=\int_{-1}^{1}\ln a(1-x^2)dx=\ln a\left [ x-\dfrac{x^3}{3} \right ]_{-1}^{1}=\dfrac{4}{3}\ln a<\frac{4}{3}](/forum/ext/geomar/texintegr/latexrender/pictures/05a8a4c674b69a11a0a63a2496573dca.png)
 Έστω
Έστω 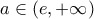 , τότε:
, τότε:![\displaystyle f(x) = \lim_{y\to +\infty} \dfrac{a^y[x+(x^2-1)\cdot {(\frac{e}{a})}^y]}{a^{y-1}[1+e^4 \cdot{(\frac{e}{a})}^{y-1}]}=ax \displaystyle f(x) = \lim_{y\to +\infty} \dfrac{a^y[x+(x^2-1)\cdot {(\frac{e}{a})}^y]}{a^{y-1}[1+e^4 \cdot{(\frac{e}{a})}^{y-1}]}=ax](/forum/ext/geomar/texintegr/latexrender/pictures/1cd45ac05af33699da8bde8d72053d53.png)
'Ομως,
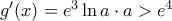 , οπότε
, οπότε  γνησίως αύξουσα.
γνησίως αύξουσα.Ο Θεός μπορεί να μην παίζει ζάρια με το σύμπαν, αλλά κάτι περίεργο συμβαίνει με τους πρώτους αριθμούς ~ Paul Erdős
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης
