Μια παραγωγίσιμη συνάρτηση
 με
με 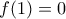 έχει την ιδιότητα :
έχει την ιδιότητα : .
.α) Να αποδείξετε ότι

β) Να υπολογίσετε το ολοκλήρωμα

γ) Αν
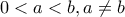 και
και 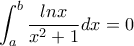 , να αποδειχθεί ότι
, να αποδειχθεί ότι  και
και 
Μπάμπης
Συντονιστής: Καρδαμίτσης Σπύρος
 με
με 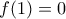 έχει την ιδιότητα :
έχει την ιδιότητα : .
.

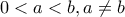 και
και 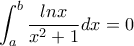 , να αποδειχθεί ότι
, να αποδειχθεί ότι  και
και 
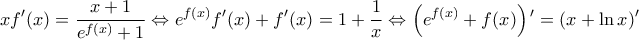
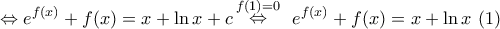
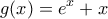 που είναι ορισμένη στο R και 1-1 (εύκολο)
που είναι ορισμένη στο R και 1-1 (εύκολο)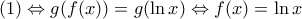

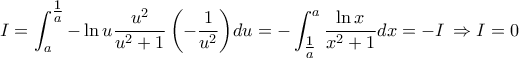
![\displaystyle{
{\rm A}\nu \,\,0 < \alpha < \beta \le 1\,\,\,\tau o\tau \varepsilon \,\,\,\int_\alpha ^\beta {\frac{{\ln x}}{{x^2 + 1}}dx\,\,\, < 0\,\,\,\alpha \phi o\upsilon \,\,} \frac{{\ln x}}{{x^2 + 1}} \le 0\,\,\,\gamma \iota \alpha \,\,\,\kappa \alpha \theta \varepsilon \,\,x \in \left[ {a,\beta } \right]\,} \displaystyle{
{\rm A}\nu \,\,0 < \alpha < \beta \le 1\,\,\,\tau o\tau \varepsilon \,\,\,\int_\alpha ^\beta {\frac{{\ln x}}{{x^2 + 1}}dx\,\,\, < 0\,\,\,\alpha \phi o\upsilon \,\,} \frac{{\ln x}}{{x^2 + 1}} \le 0\,\,\,\gamma \iota \alpha \,\,\,\kappa \alpha \theta \varepsilon \,\,x \in \left[ {a,\beta } \right]\,}](/forum/ext/geomar/texintegr/latexrender/pictures/85550d793a9658ef93655e55c381d6cd.png) (το ίσον ισχύει μόνο αν x = β =1)
(το ίσον ισχύει μόνο αν x = β =1)![\displaystyle{
{\rm A}\nu \,\,\,1 \le \alpha < \beta \,\,\,\tau o\tau \varepsilon \,\,\,\int_\alpha ^\beta {\frac{{\ln x}}{{x^2 + 1}}dx\, > 0\,\,\,\alpha \phi o\upsilon \,\,} \frac{{\ln x}}{{x^2 + 1}} \ge 0\,\,\,\gamma \iota \alpha \,\,\,\kappa \alpha \theta \varepsilon \,\,x \in \left[ {a,\beta } \right]} \displaystyle{
{\rm A}\nu \,\,\,1 \le \alpha < \beta \,\,\,\tau o\tau \varepsilon \,\,\,\int_\alpha ^\beta {\frac{{\ln x}}{{x^2 + 1}}dx\, > 0\,\,\,\alpha \phi o\upsilon \,\,} \frac{{\ln x}}{{x^2 + 1}} \ge 0\,\,\,\gamma \iota \alpha \,\,\,\kappa \alpha \theta \varepsilon \,\,x \in \left[ {a,\beta } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/bce08551c1aa34b81edc54c7be576c8b.png) (το ίσον ισχύει μόνο αν x = α =1)
(το ίσον ισχύει μόνο αν x = α =1)
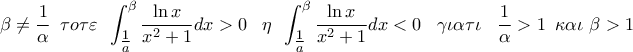
Χρήστο, ευχαριστώ !chris_gatos έγραψε:Υπήρχε και --->εδώ με μία πολύ ωραία
επεξήγηση του Μιχάλη.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης