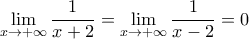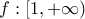 με τύπο
με τύπο 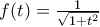 και
και  μια αρχική της
μια αρχική της  .
.Να βρεθεί το
![\lim_{x\rightarrow +\infty}[F(x+1)-F(x-1)] \lim_{x\rightarrow +\infty}[F(x+1)-F(x-1)]](/forum/ext/geomar/texintegr/latexrender/pictures/3442b9b2b0c037efe762b767d6750c47.png) .
.Ας αρχίσουμε, η
 είναι γνησίως φθίνουσα
είναι γνησίως φθίνουσα 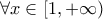 και από ΘΜΤ υπάρχει
και από ΘΜΤ υπάρχει 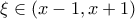 τέτοιο ώστε
τέτοιο ώστε 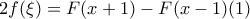
Για να υπολογισουμε το ζητούμενο όριο θα πρέπει να εκμεταλλευτούμε το κριτήριο παρεμβολής και για να γίνει αυτό πρέπει να δημιουργήσουμε ανισότητα με (''
 ''). Είναι σωστό όμως να πουμε πως
''). Είναι σωστό όμως να πουμε πως 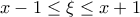 και να συνεχίσουμε με χρήση ανισοϊσοτητας ; Με προβληματίζει επειδή προηγουμένως από το ΘΜΤ προεκυψε πως το
και να συνεχίσουμε με χρήση ανισοϊσοτητας ; Με προβληματίζει επειδή προηγουμένως από το ΘΜΤ προεκυψε πως το  ανήκει στο ανοιχτό διάστημα αυτού.
ανήκει στο ανοιχτό διάστημα αυτού.Γενικότερα μπορώ να χρησιμοποιώ ανισότητες τέτοιας μορφής οι οποίες προέρχονται από τη διάταξη του ξ;
Σας ευχαριστώ

 τότε κατά μείζονα λόγο ισχύει
τότε κατά μείζονα λόγο ισχύει  .
. 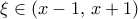 τέτοιο ώστε... "
τέτοιο ώστε... "![\xi \in [x-1,\, x+1] \xi \in [x-1,\, x+1]](/forum/ext/geomar/texintegr/latexrender/pictures/87a6ecfcb788eb158e329ffd92adc3e4.png) τέτοιο ώστε ... "
τέτοιο ώστε ... " 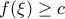 , και από ΘΜΤ έχουμε βγάλει
, και από ΘΜΤ έχουμε βγάλει 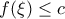 , μπορούμε να ισχυριστούμε πως
, μπορούμε να ισχυριστούμε πως 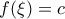 ; Μου φαίνεται περίεργο να ισχυει επειδή κάνοντας χρήση του (''
; Μου φαίνεται περίεργο να ισχυει επειδή κάνοντας χρήση του ('' '') από το ΘΜΤ δεν προκύπτει κάτι τέτοιο
'') από το ΘΜΤ δεν προκύπτει κάτι τέτοιο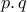 ισχύει ακριβώς ένα από τα
ισχύει ακριβώς ένα από τα  . Τώρα, αν ισχύει
. Τώρα, αν ισχύει 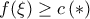 και
και 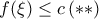 τότε
τότε 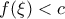 λόγω της
λόγω της 
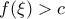 λόγω της
λόγω της 

 , το ζητούμενο είναι ίσο με
, το ζητούμενο είναι ίσο με 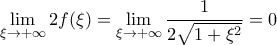
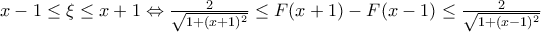 αν καταλαβα καλα, η ισοτητα αποκλειεται να ισχυει, ωστοσο δεν ειναι λαθος να την παρουσιασουμε, σωστα;
αν καταλαβα καλα, η ισοτητα αποκλειεται να ισχυει, ωστοσο δεν ειναι λαθος να την παρουσιασουμε, σωστα;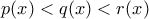 και αν
και αν 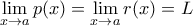 , τότε το
, τότε το 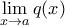 υπάρχει και μάλιστα
υπάρχει και μάλιστα 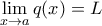 .
.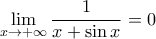 , μπορείς να χρησιμοποιήσεις τις
, μπορείς να χρησιμοποιήσεις τις 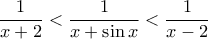 και μετά
και μετά