Δίνεται η παραγωγίσιμη συνάρτηση
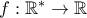 με
με 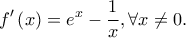
Το ένα υποερώτημα ήταν: Να μελετήσετε την
 ως προς τα τοπικά ακρότατα.
ως προς τα τοπικά ακρότατα.  Η
Η  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο 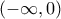 με
με 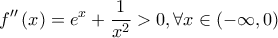 και η
και η  συνεχής στο
συνεχής στο 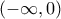 , άρα η
, άρα η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 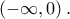 Η
Η  είναι συνεχής και γνησίως αύξουσα στο
είναι συνεχής και γνησίως αύξουσα στο 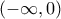 , επομένως
, επομένως 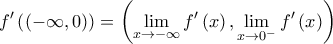 , όπου:
, όπου: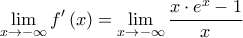
και αφού
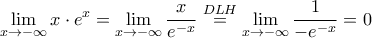 , έπεται ότι :
, έπεται ότι :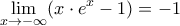 και συνεπώς
και συνεπώς 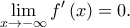
Και
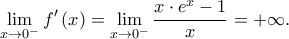
Επομένως
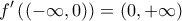 και άρα η
και άρα η  δεν έχει ρίζα στο
δεν έχει ρίζα στο 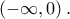 Αν η
Αν η  παρουσίαζε τοπικό ακρότατο σε κάποιο
παρουσίαζε τοπικό ακρότατο σε κάποιο 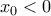 , τότε αφού είναι παραγωγίσιμη στο
, τότε αφού είναι παραγωγίσιμη στο  , από Θ. Fermat θα ήταν
, από Θ. Fermat θα ήταν 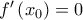 , άτοπο.
, άτοπο. Η
Η  είναι συνεχής και παραγωγίσιμη στο
είναι συνεχής και παραγωγίσιμη στο  με
με 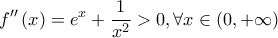 , άρα η
, άρα η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 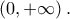 Η
Η  είναι συνεχής και γνησίως αύξουσα στο
είναι συνεχής και γνησίως αύξουσα στο  , επομένως:
, επομένως: 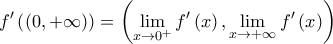 , όπου:
, όπου: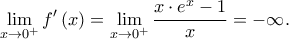
Και
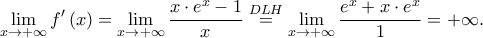
Επομένως
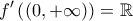 και άρα η
και άρα η  έχει ρίζα
έχει ρίζα 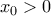 και αφού είναι γνησίως αύξουσα στο
και αφού είναι γνησίως αύξουσα στο  , το
, το  είναι μοναδικό.
είναι μοναδικό. Επίσης:
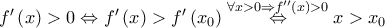
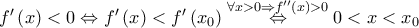
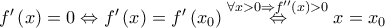
και η
 είναι συνεχής στο
είναι συνεχής στο  , άρα η
, άρα η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο ![\left ( 0, x_{0}\right ] \left ( 0, x_{0}\right ]](/forum/ext/geomar/texintegr/latexrender/pictures/5ed7f773aab66e223bf212678d5757dc.png) και γνησίως αύξουσα στο
και γνησίως αύξουσα στο 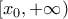 , παρουσιάζοντας τοπικό ελάχιστο στο μοναδικό αυτό
, παρουσιάζοντας τοπικό ελάχιστο στο μοναδικό αυτό 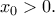

 προφανώς
προφανώς 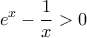 , οπότε η
, οπότε η  δεν έχει τοπικά ακρότατα στο
δεν έχει τοπικά ακρότατα στο 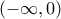 .
.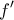 προκύπτουν εύκολα, χωρίς να κάνουμε ομώνυμα.
προκύπτουν εύκολα, χωρίς να κάνουμε ομώνυμα.

![\displaystyle{\begin{tikzpicture} \draw[>->, line width=1.5pt] (0, 0) -- (0, 0.5); \end{tikzpicture}} \displaystyle{\begin{tikzpicture} \draw[>->, line width=1.5pt] (0, 0) -- (0, 0.5); \end{tikzpicture}}](/forum/ext/geomar/texintegr/latexrender/pictures/8963ceee54fe59151a9a04eb81863945.png) ,
, ![\displaystyle{\begin{tikzpicture} \draw[<-<, line width=1.5pt] (0, 0) -- (0, 0.5); \end{tikzpicture}} \displaystyle{\begin{tikzpicture} \draw[<-<, line width=1.5pt] (0, 0) -- (0, 0.5); \end{tikzpicture}}](/forum/ext/geomar/texintegr/latexrender/pictures/436b89fedd5cf784c0d6c34abf152ce1.png)
