ma128 έγραψε: ↑Τετ Μαρ 09, 2022 4:56 pm
ΜΕ ΔΕΔΟΜΕΝΟ ΟΤΙ:

β)Απο Θ.Rolle για την

στο
![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png)
, προκύπτει οτι υπάρχει

ώστε
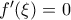
Αφού
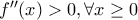
Έπεται οτι η
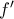
είναι γνησίως αύξουσα στο διάστημα αυτό , και άρα η
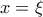
είναι η μοναδική της ρίζα.
Επομένως, ισχύει:
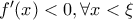
και
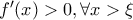
Άρα, η

είναι γνησίως φθίνουσα στο
![[0,\xi] [0,\xi]](/forum/ext/geomar/texintegr/latexrender/pictures/691a2e9abf2eb71759de66d14b9cda0d.png)
και γνησίως αύξουσα στο
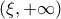
Έτσι παρουσιάζει τοπικό μέγιστο για

το

και ολικό ελάχιστο για
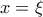
το
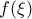
.
α)Απο ΘΜΤ για την

στα
![[1,2] [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/f79408e5ca998cd53faf44af31e6eb45.png)
και
![[2,x] [2,x]](/forum/ext/geomar/texintegr/latexrender/pictures/7ad69a8ebfece27b0fbaa6dea6962483.png)
, υπάρχουν
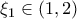
και
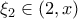
τέτοια ώστε:
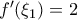
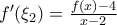
Ισχύει:

και
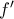
αύξουσα
Επομενως:
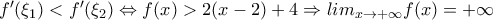
γ)Θεωρώ:
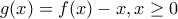
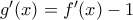
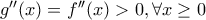
Παρατηρώ ότι:
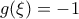
και
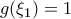
Επομένως, απο θ.Μπολζάνο , υπάρχει, και λόγω μονοτονίας είναι μοναδικό,
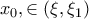
, ώστε
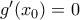
Άρα η

είναι γνησίως φθίνουσα για

και γνησίως αύξουσα για

Δηλαδή, για
![x\in [0,2] x\in [0,2]](/forum/ext/geomar/texintegr/latexrender/pictures/ab4b24411a5ed26ec37e0c77338f254e.png)
, ισχύει:
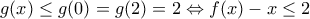
δ)
ΜΕ ΕΠΙΦΥΛΑΞΗ
Ο παρανομαστής είναι:
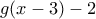
, και γνωρίζω ότι:
![g(x-3)\leq 2, x\in[3,5] g(x-3)\leq 2, x\in[3,5]](/forum/ext/geomar/texintegr/latexrender/pictures/29ef579f8f2bc6d9aa9383101d355511.png)
.
Επομένως:
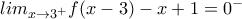
Ενώ, ο αριθμητής είναι:
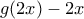
Θεωρώ:
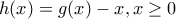
Παρατηρώ οτι:
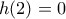
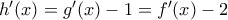
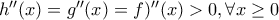
Παρατηρώ, ότι:
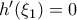
και λόγω μονοτονίας αποτελεί μοναδική ρίζα.
Άρα, η

είναι φθίνουσα για
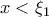
και αύξουσα, για

.
Επομένως ισχύει:
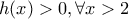
Και έτσι:
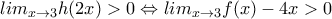
Τελικά:
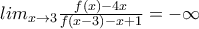
ε) Προκύπτει άμεσα απο την ανισότητα του γ)
![\int _0^2f(x)dx<\int _0^2(x+2)dx=[\frac{x^2}{2}+2x]_0^2=6 \int _0^2f(x)dx<\int _0^2(x+2)dx=[\frac{x^2}{2}+2x]_0^2=6](/forum/ext/geomar/texintegr/latexrender/pictures/3d4c96daef5f427f3442508d6a4e44cf.png)
Μια παρατήρηση πρώτα: Δεν γράφουμε ότι "η συνάρτηση είναι γνησίως αύξουσα, (φθίνουσα), για χ...." Δεν υπάρχει η έννοια της μονοτονίας σε κάποιον αριθμό χ.
Καλή είναι η λύση σου

εκτός, ίσως, από το δ), στο οποίο θα μπορούσαμε να απαντήσουμε ως εξής:
Για το όριο του παρονομαστή έχουμε:
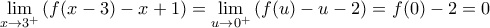
,
με
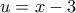
και εφόσον η

συνεχής.
Από το γ) ερώτημα έχουμε ότι
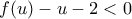
, για

και "κοντά" στο

.
Άρα το όριο του παρονομαστή είναι

και οι τιμές του για

"κοντά" στο

αρνητικές.
Για το όριο του αριθμητή έχουμε:
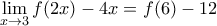
, λόγω συνέχειας της

.
Έχουμε δείξει στο α) ότι
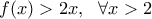
και έτσι
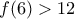
.
Άρα το όριο του αριθμητή είναι θετικός αριθμός, οπότε το ζητούμενο όριο θα είναι

Και ένα σχόλιο....
Τελικά έχουμε μία καλή άσκηση και έτσι οφείλουμε να συγχωρήσουμε το λάθος δεδομένο της "Πυθαγόρειας Τριάδας" καθώς και τη σιωπή της!
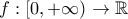 μια δύο φορές παραγωγίσιμη συνάρτηση στο διάστημα
μια δύο φορές παραγωγίσιμη συνάρτηση στο διάστημα 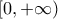 με:
με:
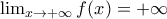
 παρουσιάσει τοπικό μέγιστο και ένα ολικό ελάχιστο.
παρουσιάσει τοπικό μέγιστο και ένα ολικό ελάχιστο.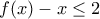 για κάθε
για κάθε ![x \in [0,2] x \in [0,2]](/forum/ext/geomar/texintegr/latexrender/pictures/98a52bc3672363c5016ed2c612f95a99.png) . Έπειτα να εξηγήσετε γεωμετρικά το αποτέλεσμα.
. Έπειτα να εξηγήσετε γεωμετρικά το αποτέλεσμα.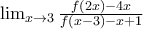
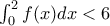

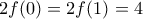
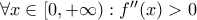
![f(x)-x>2, x \in [0,2] f(x)-x>2, x \in [0,2]](/forum/ext/geomar/texintegr/latexrender/pictures/15c6b95a8be3849c80de39e774e8db85.png)
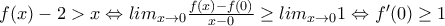
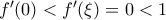
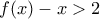 ". Ο ίδιος όμως χρησιμοποιείς το "για κάθε", όπως φαίνεται από το γεγονός ότι χρειάζεσαι ΟΛΑ τα
". Ο ίδιος όμως χρησιμοποιείς το "για κάθε", όπως φαίνεται από το γεγονός ότι χρειάζεσαι ΟΛΑ τα  κοντά στο
κοντά στο  όταν παίρνεις όριο.
όταν παίρνεις όριο. , έχουμε:
, έχουμε: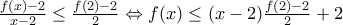

 , είναι μονότονη. Εδώ
, είναι μονότονη. Εδώ 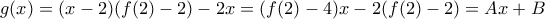 και η μονοτονία δεν θέλει θεωρίες.
και η μονοτονία δεν θέλει θεωρίες. " προκύπτει από το αριστερό μέλος με πολλαπλασιασμό επί
" προκύπτει από το αριστερό μέλος με πολλαπλασιασμό επί  . Σωστά; Όμως έχουμε
. Σωστά; Όμως έχουμε 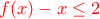 για κάθε
για κάθε ![x \in [0,2]} x \in [0,2]}](/forum/ext/geomar/texintegr/latexrender/pictures/412b2081f6fcf5c6c5d3feabad188206.png) . Έπειτα να εξηγήσετε γεωμετρικά το αποτέλεσμα.
. Έπειτα να εξηγήσετε γεωμετρικά το αποτέλεσμα.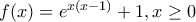





![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) , προκύπτει οτι υπάρχει
, προκύπτει οτι υπάρχει  ώστε
ώστε 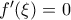
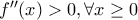
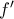 είναι γνησίως αύξουσα στο διάστημα αυτό , και άρα η
είναι γνησίως αύξουσα στο διάστημα αυτό , και άρα η 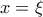 είναι η μοναδική της ρίζα.
είναι η μοναδική της ρίζα.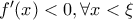 και
και 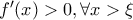
![[0,\xi] [0,\xi]](/forum/ext/geomar/texintegr/latexrender/pictures/691a2e9abf2eb71759de66d14b9cda0d.png) και γνησίως αύξουσα στο
και γνησίως αύξουσα στο 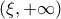
 το
το  και ολικό ελάχιστο για
και ολικό ελάχιστο για 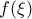 .
.![[1,2] [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/f79408e5ca998cd53faf44af31e6eb45.png) και
και ![[2,x] [2,x]](/forum/ext/geomar/texintegr/latexrender/pictures/7ad69a8ebfece27b0fbaa6dea6962483.png) , υπάρχουν
, υπάρχουν 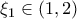 και
και 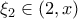 τέτοια ώστε:
τέτοια ώστε: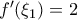
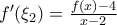
 και
και 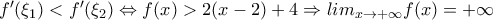
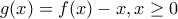
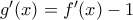
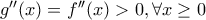
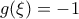 και
και 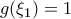
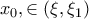 , ώστε
, ώστε 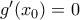
 και γνησίως αύξουσα για
και γνησίως αύξουσα για 
![x\in [0,2] x\in [0,2]](/forum/ext/geomar/texintegr/latexrender/pictures/ab4b24411a5ed26ec37e0c77338f254e.png) , ισχύει:
, ισχύει: 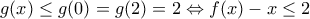
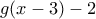 , και γνωρίζω ότι:
, και γνωρίζω ότι: ![g(x-3)\leq 2, x\in[3,5] g(x-3)\leq 2, x\in[3,5]](/forum/ext/geomar/texintegr/latexrender/pictures/29ef579f8f2bc6d9aa9383101d355511.png) .
.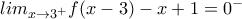
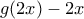
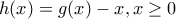
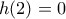
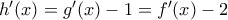
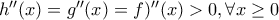
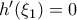 και λόγω μονοτονίας αποτελεί μοναδική ρίζα.
και λόγω μονοτονίας αποτελεί μοναδική ρίζα. είναι φθίνουσα στο
είναι φθίνουσα στο ![[, \xi_1] [, \xi_1]](/forum/ext/geomar/texintegr/latexrender/pictures/a3f29b4893915de44a8ab0fddc7b8d17.png) και αύξουσα στο
και αύξουσα στο 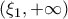 .
.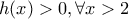
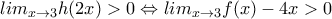
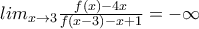
![\int _0^2f(x)dx<\int _0^2(x+2)dx=[\frac{x^2}{2}+2x]_0^2=6 \int _0^2f(x)dx<\int _0^2(x+2)dx=[\frac{x^2}{2}+2x]_0^2=6](/forum/ext/geomar/texintegr/latexrender/pictures/3d4c96daef5f427f3442508d6a4e44cf.png)
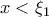 και αύξουσα, για
και αύξουσα, για  .
.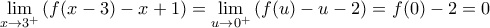 ,
, 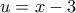 και εφόσον η
και εφόσον η 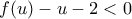 , για
, για  και "κοντά" στο
και "κοντά" στο  αρνητικές.
αρνητικές.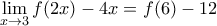 , λόγω συνέχειας της
, λόγω συνέχειας της 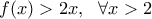 και έτσι
και έτσι 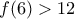 .
.