Αναχρονιστική εφαπτόμενη
Συντονιστής: Καρδαμίτσης Σπύρος
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3345
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Αναχρονιστική εφαπτόμενη
Είστε μαθηματικός σε κάποια Ευρωπαϊκή Αυλή λίγο μετά την εισαγωγή/ανακάλυψη της Αναλυτικής Γεωμετρίας* ... και η νεαρή Πριγκήπισσα σας ρωτάει αν μπορείτε να της δείξετε έναν τρόπο εύρεσης της εξίσωσης εφαπτομένης σε τυχόν σημείο πολυωνυμικής καμπύλης: ζωγραφίζει ίσως μία συγκεκριμένη τριτοβάθμια ή τεταρτοβάθμια, φέρει την εφαπτομένη σε τυχόν σημείο ... και επιτακτικά ζητάει εξίσωση, τι θα της λέγατε;
*τουτέστιν λίγο πριν την επινόηση του Διαφορικού Λογισμού και της παραγώγου
*τουτέστιν λίγο πριν την επινόηση του Διαφορικού Λογισμού και της παραγώγου
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Λέξεις Κλειδιά:
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13300
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Αναχρονιστική εφαπτόμενη
Η εξίσωση της εφαπτομένης τηςgbaloglou έγραψε: ↑Πέμ Νοέμ 30, 2023 10:49 pmΕίστε μαθηματικός σε κάποια Ευρωπαϊκή Αυλή λίγο μετά την εισαγωγή/ανακάλυψη της Αναλυτικής Γεωμετρίας* ... και η νεαρή Πριγκήπισσα σας ρωτάει αν μπορείτε να της δείξετε έναν τρόπο εύρεσης της εξίσωσης εφαπτομένης σε τυχόν σημείο πολυωνυμικής καμπύλης: ζωγραφίζει ίσως μία συγκεκριμένη τριτοβάθμια ή τεταρτοβάθμια, φέρει την εφαπτομένη σε τυχόν σημείο ... και επιτακτικά ζητάει εξίσωση, τι θα της λέγατε;
*τουτέστιν λίγο πριν την επινόηση του Διαφορικού Λογισμού και της παραγώγου
 στο
στο  είναι:
είναι: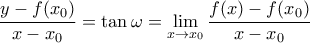
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3345
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Αναχρονιστική εφαπτόμενη
Γιώργο ναι, καταφεύγεις όμως έτσι στον Διαφορικό Λογισμό, ή αν θες στην ανακάλυψη του! Κάτι χωρίς παραγώγους ή έστω όρια;george visvikis έγραψε: ↑Παρ Δεκ 01, 2023 11:28 amΑναχρονιστική εφαπτομένη.pnggbaloglou έγραψε: ↑Πέμ Νοέμ 30, 2023 10:49 pmΕίστε μαθηματικός σε κάποια Ευρωπαϊκή Αυλή λίγο μετά την εισαγωγή/ανακάλυψη της Αναλυτικής Γεωμετρίας* ... και η νεαρή Πριγκήπισσα σας ρωτάει αν μπορείτε να της δείξετε έναν τρόπο εύρεσης της εξίσωσης εφαπτομένης σε τυχόν σημείο πολυωνυμικής καμπύλης: ζωγραφίζει ίσως μία συγκεκριμένη τριτοβάθμια ή τεταρτοβάθμια, φέρει την εφαπτομένη σε τυχόν σημείο ... και επιτακτικά ζητάει εξίσωση, τι θα της λέγατε;
*τουτέστιν λίγο πριν την επινόηση του Διαφορικού Λογισμού και της παραγώγου
Η εξίσωση της εφαπτομένης τηςστο
είναι:
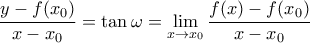
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- matha
- Γενικός Συντονιστής
- Δημοσιεύσεις: 6423
- Εγγραφή: Παρ Μάιος 21, 2010 7:40 pm
- Τοποθεσία: Θεσσαλονίκη
Re: Αναχρονιστική εφαπτόμενη
Επιτρέπεται να απαιτήσουμε ότι η εξίσωση  έχει πολλαπλή ρίζα;
έχει πολλαπλή ρίζα;
 έχει πολλαπλή ρίζα;
έχει πολλαπλή ρίζα;Μάγκος Θάνος
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3345
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Αναχρονιστική εφαπτόμενη
NAI
[Ή τουλάχιστον έτσι το βλέπω εγώ, οι κατέχοντες την Ιστορία ίσως να έχουν να πουν κάτι παραπάνω...]
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3345
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Αναχρονιστική εφαπτόμενη
Στην περίπτωση της παραβολής -- αλλά και κάθε κωνικής τομής -- είναι ξεκάθαρο, λόγω βαθμού
 , ότι μία ευθεία εφάπτεται αυτής αν και μόνον αν έχει μόνον ένα κοινό σημείο μ' αυτήν, αν και μόνον αν δηλαδή η
, ότι μία ευθεία εφάπτεται αυτής αν και μόνον αν έχει μόνον ένα κοινό σημείο μ' αυτήν, αν και μόνον αν δηλαδή η  έχει διπλή ρίζα. Στους μεγαλύτερους βαθμούς χρειάζεται ένα κάποιο 'άλμα', να σκεφθούμε δηλαδή ότι η ευθεία εφάπτεται της καμπύλης στο
έχει διπλή ρίζα. Στους μεγαλύτερους βαθμούς χρειάζεται ένα κάποιο 'άλμα', να σκεφθούμε δηλαδή ότι η ευθεία εφάπτεται της καμπύλης στο  αν και μόνον αν το
αν και μόνον αν το  είναι διπλή τουλάχιστον ρίζα της
είναι διπλή τουλάχιστον ρίζα της  : αυτό επειδή η 'ελάχιστη' αλλαγή του
: αυτό επειδή η 'ελάχιστη' αλλαγή του  οδηγεί σε δεύτερο σημείο τομής πολύ κοντά στο
οδηγεί σε δεύτερο σημείο τομής πολύ κοντά στο 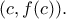
Θα μπορούσε ο παραπάνω συλλογισμός να γίνει πριν την ανακάλυψη του Διαφορικού Λογισμού, ή ακόμη και να (έχει) οδηγήσει σ' αυτήν;
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3345
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Αναχρονιστική εφαπτόμενη
Βεβαίως ... θα μπορούσε κάποιος να οδηγηθεί στην πολλαπλή ρίζα και χωρίς την παραπάνω 'κρυφή' χρήση του ορίου: στην περίπτωση πολυωνύμου τρίτου βαθμού, γνωρίζουμε 'εμπειρικά' ότι η εφαπτομένη σε τυχόν σημείο τέμνει την τριτοβάθμια σε ένα ακριβώς ακόμη σημείο, άρα μπορούμε να γράψουμεgbaloglou έγραψε: ↑Σάβ Δεκ 02, 2023 9:51 pmΣτην περίπτωση της παραβολής -- αλλά και κάθε κωνικής τομής -- είναι ξεκάθαρο, λόγω βαθμού, ότι μία ευθεία εφάπτεται αυτής αν και μόνον αν έχει μόνον ένα κοινό σημείο μ' αυτήν, αν και μόνον αν δηλαδή η
έχει διπλή ρίζα. Στους μεγαλύτερους βαθμούς χρειάζεται ένα κάποιο 'άλμα', να σκεφθογύμε δηλαδή ότι η ευθεία εφάπτεται της καμπύλης στο
αν και μόνον αν το
είναι διπλή τουλάχιστον ρίζα της
: αυτό επειδή η 'ελάχιστη' αλλαγή του
οδηγεί σε δεύτερο σημείο τομής πολύ κοντά στο
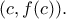
Θα μπορούσε ο παραπάνω συλλογισμός να γίνει πριν την ανακάλυψη του Διαφορικού Λογισμού, ή ακόμη και να (έχει) οδηγήσει σ' αυτήν;
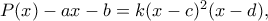 και ακολούθως να 'γενικεύσουμε' σε πολυώνυμα μεγαλύτερου βαθμού,
και ακολούθως να 'γενικεύσουμε' σε πολυώνυμα μεγαλύτερου βαθμού,  ... και να βρούμε τα
... και να βρούμε τα  και
και  εξισώνοντας συντελεστές. [Ειδική προσοχή στην τριτοβάθμια και στο σημείο καμπής της, όπου έχουμε
εξισώνοντας συντελεστές. [Ειδική προσοχή στην τριτοβάθμια και στο σημείο καμπής της, όπου έχουμε 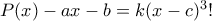 ]
] Τα παραπάνω τα σκέφτηκα φυλλομετρώντας το καινούργιο βιβλίο του φίλου και παλιού συναδέλφου Michel Helfgott, Calculus for the Natural Sciences, όπου γράφει πως η μέθοδος της εφαπτομένης δεν γενικεύεται σε τριτοβάθμιες κλπ καμπύλες: ΔΕΝ τα σκέφτηκα προ εικοσαετίας, όταν γράφαμε το άρθρο μας Finding Equations of Tangents to Conics*, στον επίλογο του οποίου γράφουμε ότι η ύπαρξη πέραν του ενός σημείων τομής (ανάμεσα σε καμπύλη και εφαπτομένη) αποτελεί αξεπέραστο εμπόδιο για την εφαρμογή της μεθόδου μας!
Παλιά όσο και η Αναλυτική Γεωμετρία θα μπορούσε να είναι αυτή η μέθοδος της πολλαπλής ρίζας! Όχι βέβαια συχνή, γι' αυτό και δεν την είχαμε υπ' όψιν μας όταν γράφαμε το παραπάνω άρθρο με τον Miquel. Μία σύγχρονη χρήση ανάλογη από πλευράς γενικότητας προς την τριτοβάθμια είναι η περίπτωση της εφαπτομένης τεταρτοβάθμιας σε δύο σημεία της, όπου
 (εδώ).
(εδώ).*ας σημειώσω εδώ ότι το άρθρο αυτό, μαζί με το Εξωτερικό Γινόμενο Διανυσμάτων, είναι με πολύ μεγάλη διαφορά τα πλέον πολυδιαβασμένα μου στο researchgate (2546 και 2324 επισκέψεις, αντίστοιχα)
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15768
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Αναχρονιστική εφαπτόμενη
Γιώργο, σε όλα τα παλιά βιβλία Αναλυτικής Γεωμετρίας που ανέπτυσσαν την ύλη τους χωρίς Απειροστικό Λογισμό (π.χ. τέτοια ήταν και τα παλιά σχολικά βιβλία στον τόπο μας), χρησιμοποιούσαν την πολλαπλή ρίζα για την εύρεση εφαπτομένης. Κάτι ανάλογο είναι στα αρχαία Ελληνικά Μαθηματικά όπου ο ορισμός ήταν: Για τον κύκλο και όμοια για τις άλλες καμπύλες "Ευθεία κύκλου εφάπτεσθαι λέγεται, ήτις απτομένη του κύκλου και εκβαλλομένη ου τέμνει τον κύκλον" (Ευκλείδου, Στοιχεία Γ'). Εδώ, αφού ο κύκλος είναι δευτεροβάθμια καμπύλη, πρόκειται για διπλή ρίζα.
Τον αντίστοιχο αυτό ορισμό χρησιμοποιεί ο Απολλώνιος στα Κωνικά του για την εύρεση εφαπτομένης στην παραβολή και στην υπερβολή, και ο Ανθέμιος στο Περί παραδόξων μηχανημάτων για την περίπτωση της έλλειψης.
Κατά σύμπτωση πριν από δύο μέρες ήμουν στην Κύπρο σε ένα συνέδριο, όπου η ομιλία μου με τίτλο Εφαπτομένη και εμβαδόν πριν από τον Απειροστικό Λογισμό, ήταν σε αυτά ακριβώς τα θέματα.
- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5285
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: Αναχρονιστική εφαπτόμενη
Καλησπέρα σε όλους. Ένα απόσπασμα από το βιβλίο της Αναλυτικής Γεωμετρίας του 1983 (Βαρουχάκης κ.α.)Mihalis_Lambrou έγραψε: ↑Δευ Δεκ 04, 2023 8:14 pm
Γιώργο, σε όλα τα παλιά βιβλία Αναλυτικής Γεωμετρίας που ανέπτυσσαν την ύλη τους χωρίς Απειροστικό Λογισμό (π.χ. τέτοια ήταν και τα παλιά σχολικά βιβλία στον τόπο μας), χρησιμοποιούσαν την πολλαπλή ρίζα για την εύρεση εφαπτομένης.
Αντίστοιχα επιλύει αναλυτικότατα και στην περίπτωση έλλειψης και υπερβολής.
ΣΧΟΛΙΟ: Θυμάμαι, αμυδρά, ότι πρόλαβα αυτήν την ύλη (ως φροντιστής). Είχαμε τότε μαθητές 1ης Δέσμης που ανταποκρίνονταν θετικά σε αυτές τις έννοιες, αν και είχαν τριπλάσια τουλάχιστον ύλη, σε σχέση με σήμερα. Δεν θυμάμαι αν κάναμε όλη τη διερεύνηση ή κάναμε μόνον παραδείγματα. Πάντως η συνθήκη της διπλής ρίζας στα σημεία επαφής ήταν σίγουρα αποδεκτή απάντηση.
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3345
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Αναχρονιστική εφαπτόμενη
Μιχάλη και Γιώργο, σας ευχαριστώ για τις απαντήσεις σας. Έχουμε παραδείγματα εύρεσης εφαπτόμενης σε τριτοβάθμια, είτε στους αρχαίους συγγραφείς είτε στα παλαιότερα συγγράμματα Αναλυτικής Γεωμετρίας;
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15768
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Αναχρονιστική εφαπτόμενη
Ναι, έχουμε πολλά παραδείγματα.
Ο Isaac Barrow στο Lectiones Geometricae το 1670 (γραμμένο στα Λατινικά αλλά υπάρχει και μεταγενέστερη μετάφραση στα Αγγλικά, δηλαδή στην μητρική του γλώσσα, από άλλον) έχει μία πρώιμη μορφή του Θεμελειώδους Θεωρήματος του Απειροστικού Λογιασμού όπου βρίσκει με Γεωμετρικό επιχείρημα την εφάπτομένη σε μεγάλη κατηγορία καμπυλών. Συγκεκριμένα στις καμπύλες της μορφής
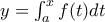
όπου
![f: [a,\,b] \longrightarrow \mathbb R f: [a,\,b] \longrightarrow \mathbb R](/forum/ext/geomar/texintegr/latexrender/pictures/295623ce6574e31dbed754adb1b7dcbd.png) συνεχής και γνήσια αύξουσα συνάρτηση. Π.χ. για την
συνεχής και γνήσια αύξουσα συνάρτηση. Π.χ. για την 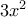 στο
στο ![[0, kati] [0, kati]](/forum/ext/geomar/texintegr/latexrender/pictures/fb120b0413654385d250a960ed87aac6.png) βρίσκουμε την εφαπτομένη της
βρίσκουμε την εφαπτομένη της  .
.H μέθοδός του είναι καταπληκτική και απόλυτα Γεωμετρική. Θα την γράψω κάποια στιγμή (την είπα άλλωστε στην ομιλία μου προχθές, στην Κύπρο) αλλά για την ώρα συγχωρείστε μου την αναβολή. Βασίζεται στον ορισμό της εφαπτομένης (όπως τον αρχαίο ελληνικό) ως ευθεία που τέμνει σε κάποιο σημείο την καμπύλη, αλλά όχι ξανά. Υπόψη ότι δεν ήξερε ολοκληςρωτικό λογισμό αφού δεν είχε ακόμη ανακαλυφθεί (από τον μαθητή του Newton) αλλά εκεί που έγραψα ολοκλήρωμα λίγο παραπάνω, ο ίδιος είχε "εμβαδόν κάτω από την
 "
"- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3345
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Αναχρονιστική εφαπτόμενη
Μιχάλη σίγουρα θα θέλαμε να την δούμε, και υπέροχη χρονοσύμπτωση (timing) να αρχίσω αυτήν την συζήτηση την ώρα που ετοιμαζόσουν για την ομιλία στην Κύπρο! Αλλά αυτό που κυρίως εννοούσα ήταν η εφαρμογή της μεθόδου πολλαπλής ρίζας τηςMihalis_Lambrou έγραψε: ↑Δευ Δεκ 04, 2023 10:43 pmΝαι, έχουμε πολλά παραδείγματα.
Ο Isaac Barrow στο Lectiones Geometricae το 1670 (γραμμένο στα Λατινικά αλλά υπάρχει και μεταγενέστερη μετάφραση στα Αγγλικά, δηλαδή στην μητρική του γλώσσα, από άλλον) έχει μία πρώιμη μορφή του Θεμελειώδους Θεωρήματος του Απειροστικού Λογιασμού όπου βρίσκει με Γεωμετρικό επιχείρημα την εφάπτομένη σε μεγάλη κατηγορία καμπυλών. Συγκεκριμένα στις καμπύλες της μορφής
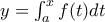
όπουσυνεχής και γνήσια αύξουσα συνάρτηση. Π.χ. για την
στο
βρίσκουμε την εφαπτομένη της
.
H μέθοδός του είναι καταπληκτική και απόλυτα Γεωμετρική. Θα την γράψω κάποια στιγμή (την είπα άλλωστε στην ομιλία μου προχθές, στην Κύπρο) αλλά για την ώρα συγχωρείστε μου την αναβολή. Βασίζεται στον ορισμό της εφαπτομένης (όπως τον αρχαίο ελληνικό) ως ευθεία που τέμνει σε κάποιο σημείο την καμπύλη, αλλά όχι ξανά. Υπόψη ότι δεν ήξερε ολοκληςρωτικό λογισμό αφού δεν είχε ακόμη ανακαλυφθεί (από τον μαθητή του Newton) αλλά εκεί που έγραψα ολοκλήρωμα λίγο παραπάνω, ο ίδιος είχε "εμβαδόν κάτω από την"
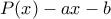 σε πολυώνυμα
σε πολυώνυμα  βαθμού τρία και πάνω ... και απαραίτητη απομάκρυνση από την αρχαιοελληνική σύλληψη της εφαπτομένης ως ευθείας που τέμνει την καμπύλη σε ένα και μόνον σημείο ... και αν έχουμε τέτοια παραδείγματα στην βιβλιογραφία...
βαθμού τρία και πάνω ... και απαραίτητη απομάκρυνση από την αρχαιοελληνική σύλληψη της εφαπτομένης ως ευθείας που τέμνει την καμπύλη σε ένα και μόνον σημείο ... και αν έχουμε τέτοια παραδείγματα στην βιβλιογραφία...Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15768
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Αναχρονιστική εφαπτόμενη
Γράφω την (Γεωμετρική, όχι Απειροστική) μέθοδο εφαπτομένης του Barrow, που υποσχέθηκα.Mihalis_Lambrou έγραψε: ↑Δευ Δεκ 04, 2023 10:43 pmΟ Isaac Barrow στο Lectiones Geometricae το 1670 (γραμμένο στα Λατινικά αλλά υπάρχει και μεταγενέστερη μετάφραση στα Αγγλικά, δηλαδή στην μητρική του γλώσσα, από άλλον) έχει μία πρώιμη μορφή του Θεμελειώδους Θεωρήματος του Απειροστικού Λογιασμού όπου βρίσκει με Γεωμετρικό επιχείρημα την εφάπτομένη σε μεγάλη κατηγορία καμπυλών. Συγκεκριμένα στις καμπύλες της μορφής
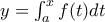
όπουσυνεχής και γνήσια αύξουσα συνάρτηση. Π.χ. για την
στο
βρίσκουμε την εφαπτομένη της
.
H μέθοδός του είναι καταπληκτική και απόλυτα Γεωμετρική. Θα την γράψω κάποια στιγμή ...
Βασίζεται στον ορισμό της εφαπτομένης (όπως τον αρχαίο ελληνικό) ως ευθεία που τέμνει σε κάποιο σημείο την καμπύλη, αλλά όχι ξανά. Υπόψη ότι δεν ήξερε ολοκληςρωτικό λογισμό αφού δεν είχε ακόμη ανακαλυφθεί (από τον μαθητή του Newton) αλλά εκεί που έγραψα ολοκλήρωμα λίγο παραπάνω, ο ίδιος είχε "εμβαδόν κάτω από την"
Έστω
 γνήσια αύξουσα συνάρτηση, όπως στο αριστερό σχήμα, και έστω
γνήσια αύξουσα συνάρτηση, όπως στο αριστερό σχήμα, και έστω 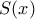 το εμβαδόν κάτω από την
το εμβαδόν κάτω από την  από το
από το  έως
έως  (δεξί σχήμα). Ο Barrow κατασκευάζει την εφαπτομένη στο σημείο
(δεξί σχήμα). Ο Barrow κατασκευάζει την εφαπτομένη στο σημείο  της
της  ως εξής:
ως εξής: Παίρνουμε μήκος
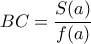 , όπου
, όπου  η προβολή του
η προβολή του  στον άξονα των
στον άξονα των  . Ισχυρίζομαι ότι η
. Ισχυρίζομαι ότι η  είναι εφαπτομένη της
είναι εφαπτομένη της  στο σημείο της
στο σημείο της  , δηλαδή ισχυρίζομαι ότι η
, δηλαδή ισχυρίζομαι ότι η  δεν τέμνει ξανά το γράφημα της
δεν τέμνει ξανά το γράφημα της  . Προς τούτο αρκεί να δείξουμε ότι αν
. Προς τούτο αρκεί να δείξουμε ότι αν  τυχαίο σημείο της
τυχαίο σημείο της  και φέρουμε το
και φέρουμε το  παράλληλο προς των άξονα των
παράλληλο προς των άξονα των  , τότε η
, τότε η  τέμνει το
τέμνει το  σε σημείο
σε σημείο  εσωτερικό του
εσωτερικό του  .
. Έχουμε (δεξί σχήμα)
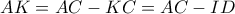 το οποίο είναι εξ ορισμού
το οποίο είναι εξ ορισμού "(το εμβαδόν κάτω από την
 μέχρι το
μέχρι το  ) μείον (το εμβαδόν κάτω από την
) μείον (το εμβαδόν κάτω από την  μέχρι το
μέχρι το  )"
)" το οποίο ισούται με το γραμμοσκιασμένο χωρίο στο αριστερό σχήμα. Επειδή η
 είναι γνήσια αύξουσα, γραμμοσκιασμένο χωρίο είναι
είναι γνήσια αύξουσα, γραμμοσκιασμένο χωρίο είναι 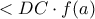 . Δηλαδή ισχύει
. Δηλαδή ισχύει 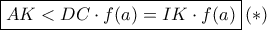 .
. Πάμε τώρα στο δεξί σχήμα. Από ομοιότητα τριγώνων έχουμε
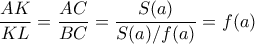 , και άρα
, και άρα 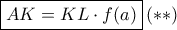
Συγκρίνοντας τις
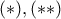 προκύπτει το ζητούμενο
προκύπτει το ζητούμενο  .
. .
- Συνημμένα
-
- Barrow efaptomeni.png (40.83 KiB) Προβλήθηκε 563 φορές
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15768
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Αναχρονιστική εφαπτόμενη
Εκανα μία τυπογραφική διόρθωση στο προηγούμενό μου ποστ, στην γραμμή που έχει το  . Όπως ήταν πριν δεν φαινόταν ο τύπος (ελέω latex), αλλά τώρα είναι ορατός.
. Όπως ήταν πριν δεν φαινόταν ο τύπος (ελέω latex), αλλά τώρα είναι ορατός.
Αξίζει ένα σχόλιο γιατί στο ποστ # ονόμασα το παραπάνω "πρώιμη μορφή του Θεμελειώδους Θεωρήματος του Απειροστικού Λογιασμού":
ονόμασα το παραπάνω "πρώιμη μορφή του Θεμελειώδους Θεωρήματος του Απειροστικού Λογιασμού":
Γνωρίζουμε σήμερα, από την εποχή του Leibniz, ότι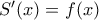 , που είναι βέβαια το Θ.Θ.Α.Λ. Με βάση το δεξί σχήμα στο προηγούμενο ποστ, αυτό μεταφράζεται ως
, που είναι βέβαια το Θ.Θ.Α.Λ. Με βάση το δεξί σχήμα στο προηγούμενο ποστ, αυτό μεταφράζεται ως 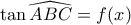 .
.
Τι σχέση έχει αυτό με τα παραπάνω του Barrow; To λοιπόν, ο Barrow λέει ακριβώς το ίδιο πράγμα διότι (στο δεξί σχήμα)
 , όπως πριν.
, όπως πριν.
Η μόνη διαφορά μεταξύ Barrow και Leibniz είναι ότι ο μεν δεύτερος μιλάει για γενικές συνεχείς συναρτήσεις ενώ ο πρώτος μόνο για γνήσια αύξουσες. Έτσι ο ατυχής Barrow έχασε την δόξα που του αξίζει.
Κατά την γνώμη μου, η συμβολή του Barrow είναι ουσιαστική γιατί ξεκαθάρισε σε πρώιμη εποχή την σχέση μεταξύ του προβλήματος του εμβαδού και του προβλήματος της εφαπτομένης, τα οποία είναι δύο όψεις του ιδίου νομίσματος.
Απευθυνόμενος ιδίως στον θεματοθέτη και φίλο Γιώργο Μπαλόγλου:
Η σχέση αυτή μεταξύ εμβαδού και εφαπτομένης είχε παρατηρηθεί και παλαιότερα σε ειδικές περιπτώσεις, από τους Fermat και Descartes. Επίσης σημαίνοντα ρόλο στην εύρεση εφαπτομένης, την πρώιμη εποχή, διαδραμάτισαν οι Johannes Hudde και René Sluse, που αξίζει να ερευνηθεί η συμβολή τους. Τα γράφω αυτά από μνήμης καθώς κάποτε είχα ψάξει το θέμα (ιδίως σχετικά με το πρόβλημα της εφαπτομένης) αλλά δεν το ολοκλήρωσα. Έχω πάντως στο αρχείο μου μερικά εξαιρετικά ενδιαφέροντα στοιχεία, κάποια άγνωστα, αλλά πολύ φοβάμαι ότι δεν πρόκειται ποτέ να ολοκληρώσω την έρευνα (φόρτος εργασίας και όγκος της υπόθεσης, γαρ).
 . Όπως ήταν πριν δεν φαινόταν ο τύπος (ελέω latex), αλλά τώρα είναι ορατός.
. Όπως ήταν πριν δεν φαινόταν ο τύπος (ελέω latex), αλλά τώρα είναι ορατός.Αξίζει ένα σχόλιο γιατί στο ποστ #
 ονόμασα το παραπάνω "πρώιμη μορφή του Θεμελειώδους Θεωρήματος του Απειροστικού Λογιασμού":
ονόμασα το παραπάνω "πρώιμη μορφή του Θεμελειώδους Θεωρήματος του Απειροστικού Λογιασμού": Γνωρίζουμε σήμερα, από την εποχή του Leibniz, ότι
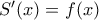 , που είναι βέβαια το Θ.Θ.Α.Λ. Με βάση το δεξί σχήμα στο προηγούμενο ποστ, αυτό μεταφράζεται ως
, που είναι βέβαια το Θ.Θ.Α.Λ. Με βάση το δεξί σχήμα στο προηγούμενο ποστ, αυτό μεταφράζεται ως 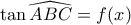 .
. Τι σχέση έχει αυτό με τα παραπάνω του Barrow; To λοιπόν, ο Barrow λέει ακριβώς το ίδιο πράγμα διότι (στο δεξί σχήμα)
 , όπως πριν.
, όπως πριν. Η μόνη διαφορά μεταξύ Barrow και Leibniz είναι ότι ο μεν δεύτερος μιλάει για γενικές συνεχείς συναρτήσεις ενώ ο πρώτος μόνο για γνήσια αύξουσες. Έτσι ο ατυχής Barrow έχασε την δόξα που του αξίζει.
Κατά την γνώμη μου, η συμβολή του Barrow είναι ουσιαστική γιατί ξεκαθάρισε σε πρώιμη εποχή την σχέση μεταξύ του προβλήματος του εμβαδού και του προβλήματος της εφαπτομένης, τα οποία είναι δύο όψεις του ιδίου νομίσματος.
Απευθυνόμενος ιδίως στον θεματοθέτη και φίλο Γιώργο Μπαλόγλου:
Η σχέση αυτή μεταξύ εμβαδού και εφαπτομένης είχε παρατηρηθεί και παλαιότερα σε ειδικές περιπτώσεις, από τους Fermat και Descartes. Επίσης σημαίνοντα ρόλο στην εύρεση εφαπτομένης, την πρώιμη εποχή, διαδραμάτισαν οι Johannes Hudde και René Sluse, που αξίζει να ερευνηθεί η συμβολή τους. Τα γράφω αυτά από μνήμης καθώς κάποτε είχα ψάξει το θέμα (ιδίως σχετικά με το πρόβλημα της εφαπτομένης) αλλά δεν το ολοκλήρωσα. Έχω πάντως στο αρχείο μου μερικά εξαιρετικά ενδιαφέροντα στοιχεία, κάποια άγνωστα, αλλά πολύ φοβάμαι ότι δεν πρόκειται ποτέ να ολοκληρώσω την έρευνα (φόρτος εργασίας και όγκος της υπόθεσης, γαρ).
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3345
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Αναχρονιστική εφαπτόμενη
Μιχάλη σ' ευχαριστούμε πολύ, προσωπικά θεωρώ ότι το να ΜΗΝ γράψεις αυτό το άρθρο -- ή ακόμη και βιβλίο -- περί Calculus shortly before Calculus (Λογισμός λίγο πριν τον Λογισμό) ... θα ήταν τραγικό!
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης
